
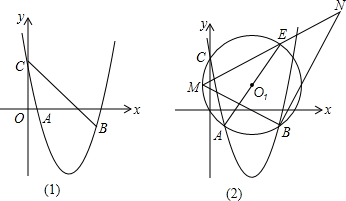
分析 (1)将点A、B的坐标代入抛物线的解析式,得到关于a、b的方程,从而可求得a、b的值;
(2)设点P的坐标为P(m,m2-6m+4),由平行四边形的面积为30可知S△CBP=15,由S△CBP=S梯形CEDP-S△CEB-S△PBD,得到关于m的方程求得m的值,从而可求得点P的坐标;
(3)首先证明△EAB∽△NMB,从而可得到NB=$\frac{3}{2}MB$,当MB为圆的直径时,NB有最大值.
解答 解:(1)将点A、B的坐标代入抛物线的解析式得:$\left\{\begin{array}{l}{a+b+4=-1}\\{25a+5b+4=-1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=1}\\{b=-6}\end{array}\right.$.
∴抛物线得解析式为y=x2-6x+4.
(2)如图所示:
设点P的坐标为P(m,m2-6m+4)
∵平行四边形的面积为30,
∴S△CBP=15,即:S△CBP=S梯形CEDP-S△CEB-S△PBD.
∴$\frac{1}{2}$m(5+m2-6m+4+1)-$\frac{1}{2}$×5×5-$\frac{1}{2}$(m-5)(m2-6m+5)=15.
化简得:m2-5m-6=0,
解得:m=6,或m=-1.
∴点P的坐标为(6,4)或(-1,11).
(3)连接AB、EB.
∵AE是圆的直径,
∴∠ABE=90°.
∴∠ABE=∠MBN.
又∵∠EAB=∠EMB,
∴△EAB∽△NMB.
∵A(1,-1),B(5,-1),
∴点O1的横坐标为3,
将x=0代入抛物线的解析式得:y=4,
∴点C的坐标为(0,4).
设点O1的坐标为(3,m),
∵O1C=O1A,
∴$\sqrt{{3}^{2}+(m-4)^{2}}=\sqrt{{2}^{2}+(m+1)^{2}}$,
解得:m=2,
∴点O1的坐标为(3,2),
∴O1A=$\sqrt{{3}^{2}+(2-4)^{2}}=\sqrt{13}$,
在Rt△ABE中,由勾股定理得:BE=$\sqrt{A{E}^{2}-A{B}^{2}}$=$\sqrt{(2\sqrt{13})^{2}-{4}^{2}}$=6,
∴点E的坐标为(5,5).
∴AB=4,BE=6.
∵△EAB∽△NMB,
∴$\frac{AB}{EB}=\frac{MB}{NB}$.
∴$\frac{4}{6}=\frac{MB}{NB}$.
∴NB=$\frac{3}{2}MB$.
∴当MB为直径时,MB最大,此时NB最大.
∴MB=AE=2$\sqrt{13}$,
∴NB=$\frac{3}{2}×2\sqrt{13}$=3$\sqrt{13}$.
点评 本题主要考查的是二次函数的综合应用,利用两点间的距离公式求得圆的半径是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
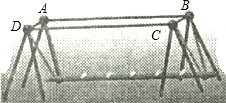 如图是一种儿童的游乐设施-儿童荡板.小明想验证这个荡板上方的四边形是否是平行四边形,现在手头只有一根足够长的绳子,请你帮助他设计一个验证方案,并说明理由.
如图是一种儿童的游乐设施-儿童荡板.小明想验证这个荡板上方的四边形是否是平行四边形,现在手头只有一根足够长的绳子,请你帮助他设计一个验证方案,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
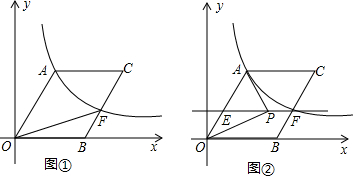
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com