
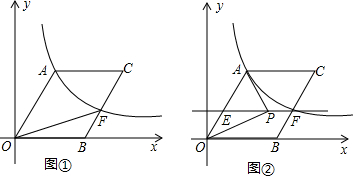
分析 (1)过点A作AH⊥x轴于点H,如图①,只需根据条件求出点A的坐标,就可求出反比例函数的解析式;
(2)过点F作FG⊥x轴于G,如图①,易证△AOH∽△FBG,根据相似三角形的性质即可求出BG、FG,从而得到点F的纵坐标,然后根据点F在反比例函数图象上,可求出点F的坐标,从而可求出OB(即AC),根据点A的坐标就可求出点C的坐标,根据OB、AH的值可求出平行四边形OACB的面积,就可得到△AOF的面积;
(3)要求△POA为钝角三角形时点P的横坐标的取值范围,只需先求出△POA为直角三角形时点P的横坐标,可分三种情况(①∠APO=90°,②∠PAO=90°,③∠AOP=90°)讨论,运用两点间的距离公式及勾股定理即可解决问题.
解答 解:(1)过点A作AH⊥x轴于点H,如图①.
∵点A在直线y=$\frac{4}{3}$x上,
∴可设A(3x,4x).
∵点A在第一象限,
∴x>0,OH=3x,AH=4x.
∵OA=10,
∴$\sqrt{(3x)^{2}+(4x)^{2}}$=10,
解得:x=2,
∴A(6,8),
∴k=6×8=48,
∴反比例函数的解析式为y=$\frac{48}{x}$;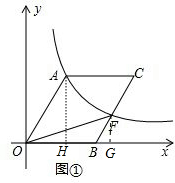
(2)过点F作FG⊥x轴于G,如图①,
∵四边形OACB是平行四边形,
∴OA=BC,AC=OB,OA∥BC,
∴∠AOH=∠FBG.
∵AH⊥x轴,FG⊥轴,
∴∠AHO=∠FGB=90°,
∴△AOH∽△FBG,
∴$\frac{OH}{BG}$=$\frac{AH}{FG}$=$\frac{OA}{BF}$.
∵点F为BC边的中点,
∴OA=BC=2BF,
∴OH=2BG=6,AH=2FG=8,
∴BG=3,FG=4.
∵点F在反比函数的图象上,
∴xF•yF=4xF=48,
∴xF=12,
∴OG=12,OB=OG-BG=12-3=9,
∴AC=OB=9,
∴点C的坐标为(6+9,8)即(15,8),
S△AOF=$\frac{1}{2}$S?OACB=$\frac{1}{2}$×OB×AH=$\frac{1}{2}$×9×8=36;
(3)满足条件的点P的横坐标x的取值范围为-2<x<8或x>$\frac{34}{3}$或x<-$\frac{16}{3}$.
提示:先考虑以P,O,A为顶点的三角形是直角三角形的情况:
∵EF∥OB,
∴点P的纵坐标为4,
∴可设点P的坐标为(x,4).
根据两点间距离公式可得:
PA2=(x-6)2+(4-8)2=x2-12x+52,
OP2=(x-0)2+(4-0)2=x2+16.
①当∠APO=90°时,如图②,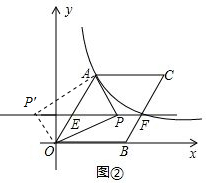
则PA2+OP2=OA2,
即x2-12x+52+x2+16=100,
整理得x2-6x-16=0
解得:x1=8,x2=-2.
∵点A的坐标为(6,8),
∴OA的中点E的坐标为(3,4),
∴当-2<x<8且x≠3时,△OPA是钝角三角形;
②当∠PAO=90°时,如图③,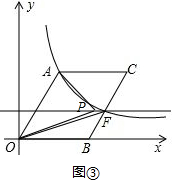
则PA2+OA2=OP2,
即x2-12x+52+100=x2+16,
解得:x=$\frac{34}{3}$,
∴当x>$\frac{34}{3}$时,△OPA是钝角三角形;
③当∠POA=90°时,如图④,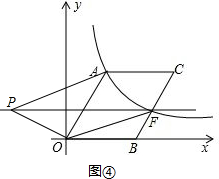
则OP2+OA2=PA2,
即x2+16+100=x2-12x+52,
解得:x=-$\frac{16}{3}$,
∴当x<-$\frac{16}{3}$时,△OPA是钝角三角形;
综上所述:当以P,O,A为顶点的三角形是钝角三角形时,
点P的横坐标x的取值范围为-2<x<8且x≠3或x>$\frac{34}{3}$或x<-$\frac{16}{3}$.
点评 本题主要考查了运用待定系数法求反比例函数的解析式、相似三角形的判定与性质、平行四边形的性质、两点间距离公式、勾股定理、解方程等知识,运用临界位置法是求取值范围最常用的一种方法,应熟练掌握.


科目:初中数学 来源: 题型:解答题
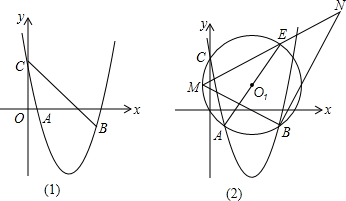
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
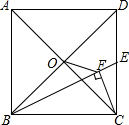 如图,正方形ABCD的边长为4,点O是对角线AC、BD的交点,点E是CD的中点,连接BE.过点C作CF⊥BE,垂足是F,连接OF,则OF的长为$\frac{2\sqrt{10}}{5}$.
如图,正方形ABCD的边长为4,点O是对角线AC、BD的交点,点E是CD的中点,连接BE.过点C作CF⊥BE,垂足是F,连接OF,则OF的长为$\frac{2\sqrt{10}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 我国古代有这样一道数学题:“枯木一根直立地上,高2丈,周3尺,有葛藤自根缠绕而上,5周而达其顶.问葛藤之长几何?”这里1丈=10尺,葛藤之长指它的最短长度.解题时,枯木视为圆柱体(如图所示)周3尺指圆柱体底面周长3尺.那么葛藤的长是25尺.
我国古代有这样一道数学题:“枯木一根直立地上,高2丈,周3尺,有葛藤自根缠绕而上,5周而达其顶.问葛藤之长几何?”这里1丈=10尺,葛藤之长指它的最短长度.解题时,枯木视为圆柱体(如图所示)周3尺指圆柱体底面周长3尺.那么葛藤的长是25尺.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
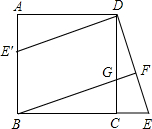 如图,在正方形ABCD中,G是CD上一点,延长BC到点E,CE=CG,连接BG并延长交DE于F.
如图,在正方形ABCD中,G是CD上一点,延长BC到点E,CE=CG,连接BG并延长交DE于F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
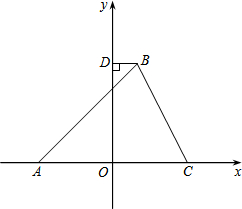 如图,在平面直角坐标系中,△ABC的顶点A在x轴负半轴上,顶点C在x轴正半轴上,顶点B在第一象限,过点B作BD⊥y轴于点D,线段OA,OC的长是一元二次方程x2-12x+36=0的两根,BC=4$\sqrt{5}$,∠BAC=45°.
如图,在平面直角坐标系中,△ABC的顶点A在x轴负半轴上,顶点C在x轴正半轴上,顶点B在第一象限,过点B作BD⊥y轴于点D,线段OA,OC的长是一元二次方程x2-12x+36=0的两根,BC=4$\sqrt{5}$,∠BAC=45°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com