
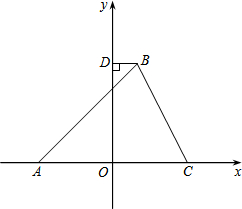
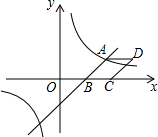
 ��ͼ����ƽ��ֱ������ϵ�У���ABC�Ķ���A��x�Ḻ�����ϣ�����C��x���������ϣ�����B�ڵ�һ���ޣ�����B��BD��y���ڵ�D���߶�OA��OC�ij���һԪ���η���x2-12x+36=0��������BC=4$\sqrt{5}$����BAC=45�㣮
��ͼ����ƽ��ֱ������ϵ�У���ABC�Ķ���A��x�Ḻ�����ϣ�����C��x���������ϣ�����B�ڵ�һ���ޣ�����B��BD��y���ڵ�D���߶�OA��OC�ij���һԪ���η���x2-12x+36=0��������BC=4$\sqrt{5}$����BAC=45�㣮���� ��1����һԪ���η���x2-12x+36=0������������ɵõ���A��C�����ꣻ
��2������B��BE��AC������ΪE���ɡ�BAC=45���֪AE=BE����BE=x���ù��ɶ����ɵ�CE=$\sqrt{80-{x}^{2}}$������AE+CE=OA+OC���ⷽ�����BE������AE-OA=OE�����������B�����꣬Ȼ�����k��ֵ��
��3���������ۣ��������������ζ�Ӧ�߳ɱ��������P�����꣮
��� �⣺��1����һԪ���η���x2-12x+36=0����ã�x1=x2=6��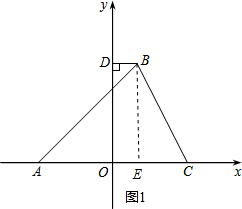
��OA=OC=6��
��A��-6��0����C��6��0����
��2����ͼ1������B��BE��AC������ΪE��
�ߡ�BAC=45�㣬
��AE=BE��
��BE=x��
��BC=4$\sqrt{5}$��
��CE=$\sqrt{80-{x}^{2}}$��
��AE+CE=OA+OC��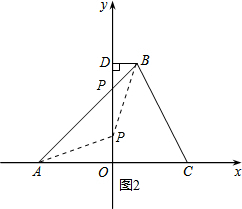 ��x+$\sqrt{80-{x}^{2}}$=12��
��x+$\sqrt{80-{x}^{2}}$=12��
�����ã�x2-12x+32=0��
��ã�x1=4������������ȥ����x2=8
��BE=8��OE=8-6=2��
��B��2��8����
��B��2��8������y=$\frac{k}{x}$����k=16��
��3�����ڣ�
��ͼ2������P��OD�ϣ�����PDB�ס�AOP��
��$\frac{OA}{DP}=\frac{OP}{DB}$��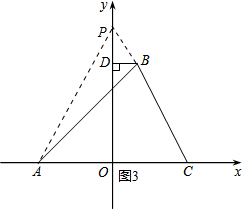 ��$\frac{6}{8-OP}=\frac{OP}{2}$
��$\frac{6}{8-OP}=\frac{OP}{2}$
��ã�OP=2��OP=6
��P��0��2����P��0��6����
��ͼ3������P��OD�Ϸ�����PDB�ס�AOP��
��$\frac{PD}{PO}=\frac{DB}{OA}$��
��$\frac{OP-8}{OP}=\frac{2}{6}$��
��ã�OP=12��
��P��0��12����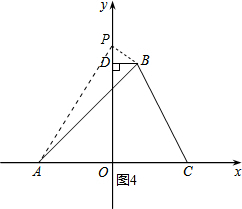 ��ͼ4������P��OD�Ϸ�����BDP�ס�AOP��
��ͼ4������P��OD�Ϸ�����BDP�ס�AOP��
��$\frac{PD}{OA}=\frac{DB}{OP}$��
��$\frac{OP-8}{6}=\frac{2}{OP}$��
��ã�OP=4+2$\sqrt{7}$��OP=4-2$\sqrt{7}$������������ȥ����
��P��0��4+2$\sqrt{7}$����
��ͼ5������P��y�Ḻ���ᣬ��PDB�ס�AOP��
��$\frac{PD}{OA}=\frac{DB}{OP}$����$\frac{OP+8}{6}=\frac{2}{OP}$����ã�OP=-4+2$\sqrt{7}$��-4-2$\sqrt{7}$������������ȥ������P������Ϊ��0��4-2$\sqrt{7}$��
���P����������0��2����0��6����0��12����0��4+2$\sqrt{7}$����0��4-2$\sqrt{7}$����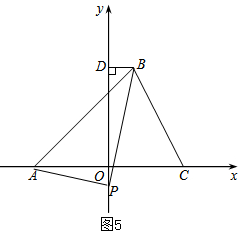
���� ������Ҫ������һԪ���η��̵Ľⷨ��������ꡢ����ͼ���ϡ����������ε��ж��������Լ��������۵���ѧ˼�뷽�����ۺ����ã���3С�����ѵ㣬ͨ�����������ε����ʷ��������г�����ʽ�ǽ������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
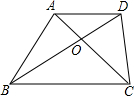
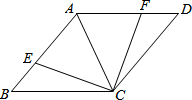 ��ͼ��AC������ABCD�ĶԽ��ߣ���E��F�ֱ���AB��AD�ϣ���AE=AF����֤��CE=CF��
��ͼ��AC������ABCD�ĶԽ��ߣ���E��F�ֱ���AB��AD�ϣ���AE=AF����֤��CE=CF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������ABCD�У�AD��BC��AB��AC��AB=AC��BD=BC����AD=$\sqrt{2}$�������ε������$\frac{5+3\sqrt{3}}{2}$��
��ͼ������ABCD�У�AD��BC��AB��AC��AB=AC��BD=BC����AD=$\sqrt{2}$�������ε������$\frac{5+3\sqrt{3}}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪һ�κ���y=$\frac{3}{2}$x-3�뷴��������y=$\frac{k}{x}$��ͼ���ཻ�ڵ�A��4��n������x���ཻ�ڵ�B��
��ͼ����֪һ�κ���y=$\frac{3}{2}$x-3�뷴��������y=$\frac{k}{x}$��ͼ���ཻ�ڵ�A��4��n������x���ཻ�ڵ�B���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪������ABCD��AB=CD=4��BC=AD=6����A=��B=��C=��D=90�㣬EΪCD�ߵ��е㣬PΪ������ABCD���ϵĶ��㣬����P��A����������A��B��C��E�˶���E��ֹͣ�����P������·��Ϊx����APE�����Ϊy��
��ͼ����֪������ABCD��AB=CD=4��BC=AD=6����A=��B=��C=��D=90�㣬EΪCD�ߵ��е㣬PΪ������ABCD���ϵĶ��㣬����P��A����������A��B��C��E�˶���E��ֹͣ�����P������·��Ϊx����APE�����Ϊy���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com