练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    13．我国古代有这样一道数学题：“枯木一根直立地上，高2丈，周3尺，有葛藤自根缠绕而上，5周而达其顶．问葛藤之长几何？”这里1丈=10尺，葛藤之长指它的最短长度．解题时，枯木视为圆柱体（如图所示）周3尺指圆柱体底面周长3尺．那么葛藤的长是25尺．

    分析 这种立体图形求最短路径问题，可以展开成为平面内的问题解决，展开后可转化下图，所以是个直角三角形求斜边的问题，根据勾股定理可求出．

    解答 解：如图，

    一条直角边（即枯木的高）长20尺，
    另一条直角边长5×3=15（尺），
    因此葛藤长$\sqrt{2{0}^{2}+1{5}^{2}}$=25
    故答案为：25．

    点评 本题考查了平面展开最短路径问题，关键是把立体图形展成平面图形，本题是展成平面图形后为直角三角形按照勾股定理可求出解．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    3．解方程（组）
    （1）2x-5=11
    （2）$\left\{\begin{array}{l}{x=3y}\\{x+3y=18}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．在同一平面直角坐标系中，若一次函数y=-x+1与y=2x+4的图象交于点M，则点M的坐标为（　　）
    A．（-1，-2）B．（-1，2）C．（2，1）D．（-2，1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

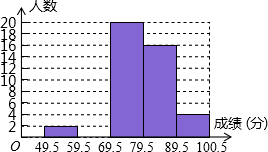    1．某班数学科代表小红对本班上学期期末考试成绩作了统计分析，绘制成如下频数，频率统计表和频率分布直方图．请你根据图表中提供的信息解答下列问题，
    （1）频数频率表中的a=8b=0.08；
    （2）补全频数分布直方图；
    （3）小红在班上任选一名同学，该同学数学成绩不低于80分的概率是多少？
    分组49.5-59.559.5-69.569.5-79.579.5-89.589.5-100.5合计
    频数2a2016450
    频率0.040.160.40.32b1

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．将“对顶角相等”这个命题改写成“如果…，那么…”的形式如果两个角是对顶角，那么它们相等．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．如图①，O为坐标原点，点B在x轴的正半轴上，四边形OACB是平行四边形，OA所在直线的解析式为y=$\frac{4}{3}$x，反比例函数y=$\frac{k}{x}$（k＞0）在第一象限内的图象经过点A，与BC交于点F，已知|OA|=10，点F为BC的中点．
    （1）求反比例函数解析式；
    （2）求△AOF的面积和点C的坐标；
    （3）过点F作EF∥OB，交OA于点E（如图②），点P为直线EF上的一个动点，连接PA，PO，问是否存在这样的点P，使以P，O，A为顶点的三角形是钝角三角形？若存在，请直接写出点P的横坐标的取值范围；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．化简：$\frac{{x}^{2}+6x+9}{{x}^{2}-9}$÷$\frac{x+3}{{x}^{2}-3x}$-x+3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

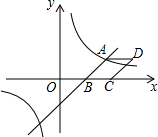    2．如图，已知一次函数y=$\frac{3}{2}$x-3与反比例函数y=$\frac{k}{x}$的图象相交于点A（4，n），与x轴相交于点B．
    （1）填空：n的值为3，k的值为12；
    （2）以AB为边作菱形ABCD，使点C在x轴正半轴上，点D在第一象限，求点D的坐标；
    （3）观察反比例函数y=$\frac{k}{x}$的图象，当y≥-2时，请直接写出自变量x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

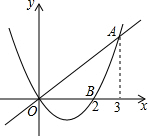    3．如图，已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A（3，2），与x轴交于点B（2，0），若0＜y1＜y2，则x的取值范围是（　　）
    A．0＜x＜2B．0＜x＜3C．2＜x＜3D．x＜0或x＞3

    查看答案和解析>>

    同步练习册答案