
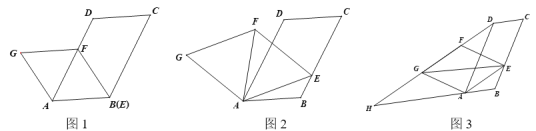
【题目】在图1,2,3中,已知□ABCD,∠ABC=120°,点E为线段BC上的动点,连接AE,以AE为边向上作菱形AEFG,且∠EAG=120°.
(1)如图1,当点E与点B重合时,∠CEF=______°;
(2)如图2,连接AF.
①填空:∠FAD_______∠EAB(填“>”,“=”,“<”);
②求证:点F在∠ABC的平分线上;
(3)如图3,连接EG,DG,并延长DG交BA的延长线于点H,当四边形AEGH是平行四边形时,求![]() 的值.
的值.
【答案】(1)60;(2)①=,②见解析;(3)3
【解析】
(1)根据菱形的性质计算即可;
(2)①证明∠DAB=∠FAE=60°,根据角的运算解答;
②作FM⊥BC于M,FN⊥BA交BA的延长线于N,证明△FAN≌△FME,根据全等三角形的性质得到FN=FM,根据角平分线的判定定理证明结论;
(3)根据直角三角形的性质得到GH=2AH,证明四边形ABEH为菱形,根据菱形的性质计算,得到答案.
解:(1)当E与点B重合时,∠EAG=120°,∵四边形GABF为菱形,
∴∠ABF=60°,∠CEF=120°-60°=60°
故答案为60°
(2)① =
∵四边形GABF为菱形;∴AF平分∠GAE,∠FAE=120°÷2=60°
∠DAB=60°,∠FAD=60°-∠DAE;∠EAB=60°-∠DAE
∴∠FAD=∠EAB
②证明:过F点做AB和BC的垂线垂足分别为M,N
由①可得三角形AEF为等边三角形
∠FAN=180°-60°-∠EAB=120°-∠EAB
∠FEM=60°+∠AEB=60°+(180°-120°-∠EAB)=120°-∠EAB
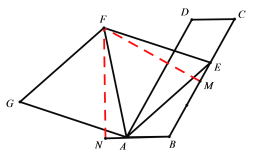
∴∠FAN=∠FEM
在FNA和FME中
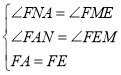
∴△FNA≌△FME(AAS)
∴FN=FM,
∴F在∠ABC的角平分线上
(3)当四边形AEGH为平行四边形时,可得GE//BH;
由四边形AEFG为菱形,可得GE平分∠FEA,∠GEA=30°
∴∠EAB=30°,AEB为等腰三角形;不妨设AB=x;可得AE=![]()
∵AE=GH;AGH为等腰三角形∴AH=![]() =3x
=3x
∠DAB=60°,∠H=30°,∴HAD为等腰三角形,可得AD=3x
BC=AD=3x
∴![]()


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的顶点A,B分别在x轴负半轴,y轴负半轴上,AD交y轴于点F,E为CD的中点.若OB=1,BD=2EF时,反比例函数y=![]() 的图象经过D,E两点,则k的值为_____.
的图象经过D,E两点,则k的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边△ABC的边长是2,以BC边上的高AB1为边作等边三角形,得到第一个等边△AB1C1;再以等边△AB1C1的B1C1边上的高AB2为边作等边三角形,得到第二个等边△AB2C2;再以等边△AB2C2的B2C2边上的高AB3为边作等边三角形,得到第三个等边△AB3C3;…,记△B1CB2的面积为S1,△B2C1B3的面积为S2,△B3C2B4的面积为S3,如此下去,则Sn=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
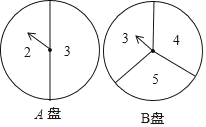
【题目】甲、乙两同学玩转盘游戏时,把质地相同的两个盘A、B分别平均分成2份和3份,并在每一份内标有数字如图.游戏规则:甲、乙两同学分别同时转动两个转盘各1次,当转盘停止后,指针所在区域的数字之积为偶数时甲胜;数字之积为奇数时乙胜.若指针恰好在分割线上,则需要重新转动转盘.
(1)用树状图或列表的方法,求甲获胜的概率;
(2)这个游戏规则对甲、乙双方公平吗?请判断并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点O是边AC上一个动点,过点O作直线EF∥BC分别交∠ACB、外角∠ACD的平分线于点E、F.
(1)若CE=8,CF=6,求OC的长;
(2)连接AE、AF.问:当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将四根长度相等的细木条首尾相接,用钉子钉成四边形ABCD,转动这个四边形,使它形状改变,当∠B=90°时,如图1,测得AC=2,当∠B=60°时,如图2,则BD=_________![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角三角形ABC中,∠ACB=900,AB=10, BC=6,在线段AB上取一点D,作DF⊥AB交AC于点F.现将△ADF沿DF折叠,使点A落在线段DB上,对应点记为A1;AD的中点E的对应点记为E1.若△E1FA1∽△E1BF,则AD= .

查看答案和解析>>
科目:初中数学 来源: 题型:
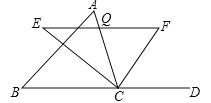
【题目】如图1是实验室中的一种摆动装置,BC在地面上,支架ABC是底边为BC的等腰直角三角形,摆动臂AD可绕点A旋转,摆动臂DM可绕点D旋转,AD=30,DM=10.
(1)在旋转过程中,
①当A,D,M三点在同一直线上时,求AM的长.
②当A,D,M三点为同一直角三角形的顶点时,求AM的长.
(2)若摆动臂AD顺时针旋转90°,点D的位置由△ABC外的点D1转到其内的点D2处,连结D1D2,如图2,此时∠AD2C=135°,CD2=60,求BD2的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com