
【题目】如图,矩形ABCD的顶点A,B分别在x轴负半轴,y轴负半轴上,AD交y轴于点F,E为CD的中点.若OB=1,BD=2EF时,反比例函数y=![]() 的图象经过D,E两点,则k的值为_____.
的图象经过D,E两点,则k的值为_____.

【答案】![]()
【解析】
根据矩形的性质以及勾股定理求出FD=![]() =
=![]() =
=![]() BC=
BC=![]() AD,则F为AD中点.如果设A(﹣a,0),a>0,则B(0,﹣1),D(a,
AD,则F为AD中点.如果设A(﹣a,0),a>0,则B(0,﹣1),D(a,![]() ),C(2a,
),C(2a,![]() ﹣1),F(0,
﹣1),F(0,![]() ),E(
),E(![]() a,
a,![]() ﹣
﹣![]() ).将E点坐标代入y=
).将E点坐标代入y=![]() ,求出k=
,求出k=![]() a,那么F(0,
a,那么F(0,![]() ).再证明△AOB∽△FOA,得出OA2=OBOF=1×
).再证明△AOB∽△FOA,得出OA2=OBOF=1×![]() =
=![]() ,求出OA=
,求出OA=![]() ,a=
,a=![]() ,进而求出k的值.
,进而求出k的值.
解:∵四边形ABCD是矩形,
∴∠ADC=∠C=90°,
∵EF=![]() BD,DE=
BD,DE=![]() CD,
CD,
∴FD=![]() =
=![]() =
=![]() BC=
BC=![]() AD,
AD,
∴F为AD中点;
设A(﹣a,0),a>0,则B(0,﹣1),D(a,![]() ),C(2a,
),C(2a,![]() ﹣1),F(0,
﹣1),F(0,![]() ),E(
),E(![]() a,
a,![]() ﹣
﹣![]() ).
).
∵反比例函数y=![]() 的图象经过E点,
的图象经过E点,
∴![]() a(
a(![]() ﹣
﹣![]() )=k,
)=k,
∴k=![]() a,
a,
∴F(0,![]() ).
).
在△AOB与△FOA中,
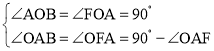 ,
,
∴△AOB∽△FOA,
∴![]() =
=![]() ,
,
∴OA2=OBOF=1×![]() =
=![]() ,
,
∴OA=![]() ,
,
∴a=![]() ,
,
∴k=![]() ×
×![]() =
=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
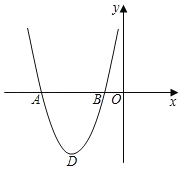
【题目】如图,在平面直角坐标系中,抛物线C1经过点A(﹣4,0)、B(﹣1,0),其顶点为![]() .
.
(1)求抛物线C1的表达式;
(2)将抛物线C1绕点B旋转180°,得到抛物线C2,求抛物线C2的表达式;
(3)再将抛物线C2沿x轴向右平移得到抛物线C3,设抛物线C3与x轴分别交于点E、F(E在F左侧),顶点为G,连接AG、DF、AD、GF,若四边形ADFG为矩形,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:①abc<0;②4ac<b2;③方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;④3a+c>0;⑤当y≥0时,x的取值范围是﹣1≤x≤3.其中结论正确的个数是( )
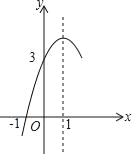
A. 1个B. 2个C. 3D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有四个分别标有数字1,-2,-3,4的小球,它们的形状、大小、质地等完全相同.小明先从盒子里随机取出一个小球,记下数字为x;放回盒子摇匀后,再随机取出一个小球,记下数字为y.
(1)小明抽到的数字是负数的概率是 .
(2)用列表法或画树状图表示出(x,y)的所有可能出现的结果;
(3)求小明两次取出小球的数字都为正数的概率;
查看答案和解析>>
科目:初中数学 来源: 题型:
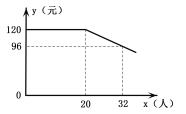
【题目】随着人们生活水平的提高,短途旅行日趋火爆.我市某旅行社推出“辽阳—葫芦岛海滨观光一日游”项目,团队人均报名费用y(元)与团队报名人数x(人)之间的函数关系如图所示,旅行社规定团队人均报名费用不能低于88元.旅行社收到的团队总报名费用为w(元).
(1)直接写出当x≥20时,y与x之间的函数关系式及自变量x的取值范围;
(2)儿童节当天旅行社收到某个团队的总报名费为3000元,报名旅游的人数是多少?
(3)当一个团队有多少人报名时,旅行社收到的总报名费最多?最多总报名费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+2x+3与x轴交于点A,B两点,点A在点B的左侧,点M为AB的中点,PQ![]() x轴交抛物线于点P,Q,点P在点Q的左侧,点Q在第一象限,以PQ,PM为邻边作PMNQ.设点P的横坐标为m.
x轴交抛物线于点P,Q,点P在点Q的左侧,点Q在第一象限,以PQ,PM为邻边作PMNQ.设点P的横坐标为m.

(1)当m=0时,求PMNO的周长;
(2)连结MQ,若MQ⊥QN时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是⊙O的直径,AB为⊙O的弦,OP⊥AD,OP与AB的延长线交于点P,过B点的切线交OP于点C.
(1)求证:∠CBP=∠ADB.
(2)若OA=2,AB=1,求线段BP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
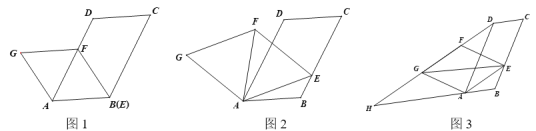
【题目】在图1,2,3中,已知□ABCD,∠ABC=120°,点E为线段BC上的动点,连接AE,以AE为边向上作菱形AEFG,且∠EAG=120°.
(1)如图1,当点E与点B重合时,∠CEF=______°;
(2)如图2,连接AF.
①填空:∠FAD_______∠EAB(填“>”,“=”,“<”);
②求证:点F在∠ABC的平分线上;
(3)如图3,连接EG,DG,并延长DG交BA的延长线于点H,当四边形AEGH是平行四边形时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com