
【题目】两个大小不同的等腰直角三角形三角板如图①所示放置,图②是由它抽象出的几何图形,B,C,E在同一条直线上,连接DC.
求证:DC⊥BE.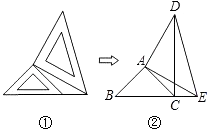
【答案】证明:∵△ABC和△ADE都是等腰直角三角形,
∴AB=AC,AE=AD,∠BAC=∠DAE=90°,
∴∠BAC+∠CAE=∠DAE+∠CAE,
即∠BAE=∠CAD,
在△ABE和△ACD中, 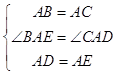 ,
,
∴△ABE≌△ACD(SAS),
∴∠ACD=∠B,
∴∠DCB=∠ACB+∠ACD=∠ACB+∠B=90°,
∴DC⊥BE.
【解析】根据等腰直角三角形的性质可得AB=AC,AE=AD,∠BAC=∠DAE=90°,再求出∠BAE=∠CAD,然后利用“边角边”证明△ABE和△ACD全等,根据全等三角形对应角相等可得∠ACD=∠B,再求出∠DCB=90°,最后根据垂直的定义证明即可.
【考点精析】关于本题考查的等腰直角三角形,需要了解等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图. 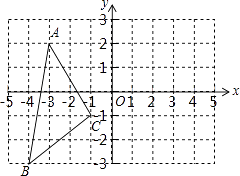
(1)在网格中画出△ABC关于y轴对称的△A1B1C1;
(2)写出△ABC关于x轴对称的△A2B2C2的各顶点坐标;
(3)在y轴上确定一点P,使PA+PB最短.(只需作图保留作图痕迹)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:若m2﹣2mn+2n2﹣8n+16=0,求m、n的值. 解:∵m2﹣2mn+2n2﹣8n+16=0,∴(m2﹣2mn+n2)+(n2﹣8n+16)=0
∴(m﹣n)2+(n﹣4)2=0,∴(m﹣n)2=0,(n﹣4)2=0,∴n=4,m=4.
根据你的观察,探究下面的问题:
(1)a2+b2﹣4a+4=0,则a= . b= .
(2)已知x2+2y2﹣2xy+6y+9=0,求xy的值.
(3)已知△ABC的三边长a、b、c都是正整数,且满足2a2+b2﹣4a﹣6b+11=0,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E在AB上,且BE= ![]() AB,点F是BC的中点,点G是DE的中点,延长DF,与AB的延长线交于点H.以下四个结论:
AB,点F是BC的中点,点G是DE的中点,延长DF,与AB的延长线交于点H.以下四个结论:
①FG= ![]() EH;②△DFE是直角三角形;③FG=
EH;②△DFE是直角三角形;③FG= ![]() DE;④DE=EB+BC.
DE;④DE=EB+BC.
其中正确结论的个数是( )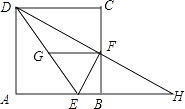
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com