
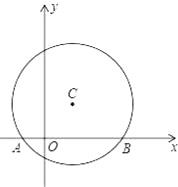
【题目】.如图,在平面直角坐标系中,以点C(1,1)为圆心,2为半径作圆,交x轴于A,B两点,点P在优弧![]() 上.
上.
(1)求出A,B两点的坐标;
(2)试确定经过A、B且以点P为顶点的抛物线解析式;
(3)在该抛物线上是否存在一点D,使线段OP与CD互相平分?若存在,求出点D的坐标;若不存在,请说明理由.
【答案】(1)![]() ,
,![]() (2)
(2)![]() 或
或![]() (3)存在
(3)存在![]() 使线段
使线段![]() 与
与![]() 互相平分
互相平分
【解析】
试题(1)根据垂径定理可得出AH=BH,然后在直角三角形ACH中可求出AH的长,再根据C点的坐标即可得出A、B两点的坐标.
(2)根据抛物线和圆的对称性,即可得出圆心C和P点必在抛物线的对称轴上,因此可得出P点的坐标为(1,3).然后可用顶点式二次函数通式来设抛物线的解析式.根据A或B的坐标即可确定抛物线的解析式.
(3)如果OP、CD互相平分,那么四边形OCPD是平行四边形.因此PC平行且相等于OD,那么D点在y轴上,且坐标为(0,2).然后将D点坐标代入抛物线的解析式中即可判定出是否存在这样的点.
试题解析:(1)如图,作CH⊥AB于点H,连接OA,OB,
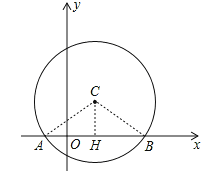
∵CH=1,半径CB=2
∴HB=![]() ,
,
故A(1-![]() ,0),B(1+
,0),B(1+![]() ,0).
,0).
(2)由圆与抛物线的对称性可知抛物线的顶点P的坐标为(1,3),
设抛物线解析式y=a(x-1)2+3,
把点B(1+![]() ,0)代入上式,解得a=-1;
,0)代入上式,解得a=-1;
∴y=-x2+2x+2.
(3)假设存在点D使线段OP与CD互相平分,则四边形OCPD是平行四边形
∴PC∥OD且PC=OD.
∵PC∥y轴,
∴点D在y轴上.
又∵PC=2,
∴OD=2,即D(0,2).
又D(0,2)满足y=-x2+2x+2,
∴点D在抛物线上
∴存在D(0,2)使线段OP与CD互相平分.


科目:初中数学 来源: 题型:
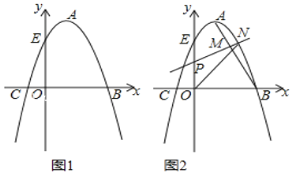
【题目】如图1,抛物线的顶点A的坐标为(1,4),抛物线与x轴相交于B、C两点,与y轴交于点E(0,3).
(1)求抛物线的表达式;
(2)已知点F(0,﹣3),在抛物线的对称轴上是否存在一点G,使得EG+FG最小,如果存在,求出点G的坐标;如果不存在,请说明理由.
(3)如图2,连接AB,若点P是线段OE上的一动点,过点P作线段AB的垂线,分别与线段AB、抛物线相交于点M、N(点M、N都在抛物线对称轴的右侧),当MN最大时,求△PON的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某市初中学生课外阅读情况,调查小组对该市这学期初中学生阅读课外书籍的册数进行了抽样调查,并根据调查结果绘制成如下统计图.
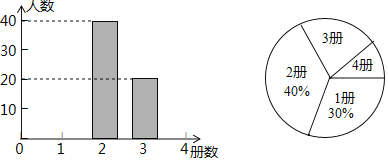
根据统计图提供的信息,解答下列问题:
(1)本次抽样调查的样本容量是 ;
(2)补全条形统计图;
(3)该市共有12000名初中生,估计该市初中学生这学期课外阅读超过2册的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
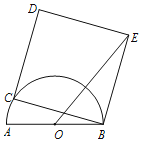
【题目】如图,点C是半圆![]() 上一动点,以BC为边作正方形BCDE,使
上一动点,以BC为边作正方形BCDE,使![]() 在正方形内,连OE,若AB=4cm,则OD的最大值为_____________cm.
在正方形内,连OE,若AB=4cm,则OD的最大值为_____________cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是![]()
![]()

A. 55° B. 60° C. 65° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
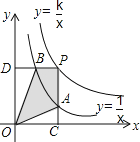
【题目】反比例函数y=![]() 和y=
和y=![]() 在第一象限内的图象如图所示,点P在y=
在第一象限内的图象如图所示,点P在y=![]() 的图象上,PC⊥x轴,交y=
的图象上,PC⊥x轴,交y=![]() 的图象于点A,PD⊥y轴,交y=
的图象于点A,PD⊥y轴,交y=![]() 的图象于点B.当点P在y=
的图象于点B.当点P在y=![]() 的图象上运动时,以下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;④当点A是PC的中点时,点B一定是PD的中点.其中一定正确的是( )
的图象上运动时,以下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;④当点A是PC的中点时,点B一定是PD的中点.其中一定正确的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
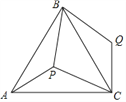
【题目】如图,点P是等边三角形ABC内一点,且PA=3,PB=4,PC=5,若将△APB绕着点B逆时针旋转后得到△CQB,则∠APB的度数 ______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
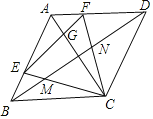
【题目】如图,已知边长为4的菱形ABCD中,AC=BC,E,F分别为AB,AD边上的动点,满足BE=AF,连接EF交AC于点G,CE、CF分别交BD与点M,N,给出下列结论:①∠AFC=∠AGE;②EF=BE+DF;③△ECF面积的最小值为3![]() ,④若AF=2,则BM=MN=DN;⑤若AF=1,则EF=3FG;其中所有正确结论的序号是_____.
,④若AF=2,则BM=MN=DN;⑤若AF=1,则EF=3FG;其中所有正确结论的序号是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
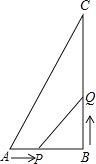
【题目】如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,设移动的时间为ts.
(1)如果P、Q分别从A、B同时出发,若t=3s,求四边形APQC的面积.
(2)如果P、Q分别从A、B同时出发,当△PBQ的面积等于8cm2时,求t的值.
(3)若△ABC与△BPQ相似,求t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com