
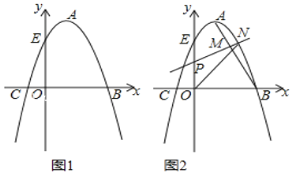
【题目】如图1,抛物线的顶点A的坐标为(1,4),抛物线与x轴相交于B、C两点,与y轴交于点E(0,3).
(1)求抛物线的表达式;
(2)已知点F(0,﹣3),在抛物线的对称轴上是否存在一点G,使得EG+FG最小,如果存在,求出点G的坐标;如果不存在,请说明理由.
(3)如图2,连接AB,若点P是线段OE上的一动点,过点P作线段AB的垂线,分别与线段AB、抛物线相交于点M、N(点M、N都在抛物线对称轴的右侧),当MN最大时,求△PON的面积.
【答案】(1)y=﹣x2+2x+3;(2)存在,G(1,0);(3)2.
【解析】
(1)根据顶点式可求得抛物线的表达式;
(2)根据轴对称的最短路径问题,作E关于对称轴的对称点E′,连接E′F交对称轴于G,此时EG+FG的值最小,先求E′F的解析式,它与对称轴的交点就是所求的点G;
(3)如图2,先利用待定系数法求AB的解析式,过N作NH⊥x轴于H,交AB于Q,设N(m,﹣m2+2m+3),则Q(m,﹣2m+6)(1<m<3),表示NQ=﹣m2+4m﹣3,证明△QMN∽△ADB,列比例式可得MN的表达式,根据配方法可得当m=2时,MN有最大值,证明△NGP∽△ADB,同理得PG的长,从而得OP的长,根据三角形的面积公式可得结论,并将m=2代入计算即可.
(1)设抛物线的表达式为:y=a(x﹣1)2+4,
把(0,3)代入得:3=a(0﹣1)2+4,
a=﹣1,
∴抛物线的表达式为:y=﹣(x﹣1)2+4=﹣x2+2x+3;
(2)存在,如图1,作E关于对称轴的对称点E',连接E'F交对称轴于G,此时EG+FG的值最小.
∵E(0,3),∴E'(2,3),
设EF的解析式为y=k′x+b′,
把F(0,﹣3),E'(2,3)分别代入,得![]() ,解得
,解得![]() ,
,
所以E'F的解析式为:y=3x﹣3,
当x=1时,y=3×1﹣3=0,∴G(1,0);
(3)如图2.
设AB的解析式为y=k″x+b″,
把A(1,4),B(3,0)分别代入,得![]() ,解得
,解得![]() ,
,
所以AB的解析式为:y=﹣2x+6,
过N作NH⊥x轴于H,交AB于Q,
设N(m,﹣m2+2m+3),则Q(m,﹣2m+6),(1<m<3),
∴NQ=(﹣m2+2m+3)﹣(﹣2m+6)=﹣m2+4m﹣3,
∵AD∥NH,∴∠DAB=∠NQM,
∵∠ADB=∠QMN=90°,∴△QMN∽△ADB,
∴![]() ,∴
,∴![]() ,
,
∴MN![]() (m﹣2)2
(m﹣2)2![]()
![]() 0,
0,
∴当m=2时,MN有最大值;
过N作NG⊥y轴于G,
∵∠GPN=∠ABD,∠NGP=∠ADB=90°,∴△NGP∽△ADB,
∴![]() ,∴PG
,∴PG![]() NG
NG![]() m,
m,
∴OP=OG﹣PG=﹣m2+2m+3![]() m=﹣m2
m=﹣m2![]() m+3,
m+3,
∴S△PON![]() OPGN
OPGN![]() (﹣m2
(﹣m2![]() m+3)m,
m+3)m,
当m=2时,S△PON![]() 2(﹣4+3+3)=2.
2(﹣4+3+3)=2.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:
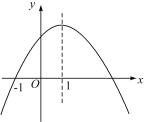
【题目】如图是二次函数y=ax2+bx+c的图象,其对称轴为x=1,下列结论:①abc>0;②2a+b=0;③4a+2b+c<0;④若(-![]() ,y1),(
,y1),(![]() ,y2)是抛物线上两点,则y1<y2, 其中结论正确的是________.
,y2)是抛物线上两点,则y1<y2, 其中结论正确的是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,港口A在观测站O的正东方向,OA=40海里,某船从港口A出发,沿北偏东15°方向航行半小时后到达B处,此时从观测站O处测得该船位于北偏东60°的方向.求该船航行的速度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着移动互联网的快速发展,基于互联网的共享单车应运而生.为了解某小区居民使用共享单车的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数分别为:17,12,15,20,17,0,7,26,17,9.
(1)这组数据的中位数是 ,众数是 ;
(2)计算这10位居民一周内使用共享单车的平均次数;
(3)若该小区有200名居民,试估计该小区居民一周内使用共享单车的总次数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲从商贩A处购买了若干斤西瓜,又从商贩B处购买了若干斤西瓜.A、B两处所购买的西瓜重量之比为3:2,然后将买回的西瓜以从A、B两处购买单价的平均数为单价全部卖给了乙,结果发现他赔钱了,这是因为( )
A. 商贩A的单价大于商贩B的单价
B. 商贩A的单价等于商贩B的单价
C. 商版A的单价小于商贩B的单价
D. 赔钱与商贩A、商贩B的单价无关
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,∠ABC=90°,AB=3,BC=4.点Q是线段AC上的一个动点,过点Q作AC的垂线交线段AB(如图1)或线段AB的延长线(如图2)于点P.
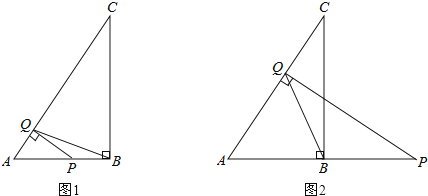
(1)当点P在线段AB上时,求证:△APQ∽△ABC;
(2)当△PQB为等腰三角形时,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读题.
材料一:若一个整数m能表示成a2-b2(a,b为整数)的形式,则称这个数为“完美数”.例如,3=22-12,9=32-02,12=42-22,则3,9,12都是“完美数”;再如,M=x2+2xy=(x+y)2-y2,(x,y是整数),所以M也是”完美数”.
材料二:任何一个正整数n都可以进行这样的分解:n=p×q(p、q是正整数,且p≤q).如果p×q在n的所有这种分解中两因数之差的绝对值最小,我们就称p×q是n的最佳分解,并且规定F(n)=![]() .例如18=1×18=2×9=3×6,这三种分解中3和6的差的绝对值最小,所以就有F(18)=
.例如18=1×18=2×9=3×6,这三种分解中3和6的差的绝对值最小,所以就有F(18)=![]() .请解答下列问题:
.请解答下列问题:
(1)8______(填写“是”或“不是”)一个完美数,F(8)= ______.
(2)如果m和n都是”完美数”,试说明mn也是完美数”.
(3)若一个两位数n的十位数和个位数分别为x,y(1≤x≤9),n为“完美数”且x+y能够被8整除,求F(n)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
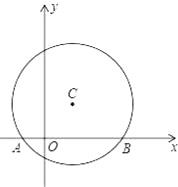
【题目】.如图,在平面直角坐标系中,以点C(1,1)为圆心,2为半径作圆,交x轴于A,B两点,点P在优弧![]() 上.
上.
(1)求出A,B两点的坐标;
(2)试确定经过A、B且以点P为顶点的抛物线解析式;
(3)在该抛物线上是否存在一点D,使线段OP与CD互相平分?若存在,求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com