
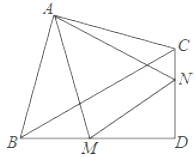
【题目】如图,在Rt△ABC和Rt△BCD中,∠BAC=∠BDC=90°,BC=4,AB=AC,∠CBD=30°,M,N分别在BD,CD上,∠MAN=45°,则△DMN的周长为_____.
【答案】2![]() +2
+2
【解析】
将△ACN绕点A逆时针旋转,得到△ABE,由旋转得出∠NAE=90°,AN=AE,∠ABE=∠ACD,∠EAB=∠CAN,求出∠EAM=∠MAN,根据SAS推出△AEM≌△ANM,根据全等得出MN=ME,求出MN=CN+BM,解直角三角形求出DC,即可求出△DMN的周长=BD+DC,代入求出答案即可.
将△ACN绕点A逆时针旋转,得到△ABE,如图:
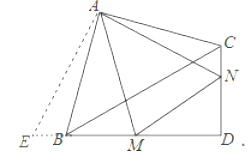
由旋转得:∠NAE=90°,AN=AE,∠ABE=∠ACD,∠EAB=∠CAN,
∵∠BAC=∠D=90°,
∴∠ABD+∠ACD=360°﹣90°﹣90°=180°,
∴∠ABD+∠ABE=180°,
∴E,B,M三点共线,
∵∠MAN=45°,∠BAC=90°,
∴∠EAM=∠EAB+∠BAM=∠CAN+∠BAM=∠BAC﹣∠MAN=90°﹣45°=45°,
∴∠EAM=∠MAN,
在△AEM和△ANM中,
 ,
,
∴△AEM≌△ANM(SAS),
∴MN=ME,
∴MN=CN+BM,
∵在Rt△BCD中,∠BDC=90°,∠CBD=30°,BC=4,
∴CD=![]() BC=2,BD=
BC=2,BD=![]() =2
=2![]() ,
,
∴△DMN的周长为DM+DN+MN=DM+DN+BM+CN=BD+DC=2![]() +2,
+2,
故答案为:2![]() +2.
+2.


科目:初中数学 来源: 题型:
【题目】规定:如果一个四边形有一组对边平行,一组邻边相等,那么称此四边形为广义菱形.根据规定判断下面四个结论:①正方形和菱形都是广义菱形;②平行四边形是广义菱形;③对角线互相垂直,且两组邻边分别相等的四边形是广义菱形;④若M、N的坐标分别为![]() P是二次函数
P是二次函数![]() 的图象上在第一象限内的任意一点,PQ垂直直线
的图象上在第一象限内的任意一点,PQ垂直直线![]() 于点Q,则四边形PMNQ是广义菱形.其中正确的是_____.(填序号)
于点Q,则四边形PMNQ是广义菱形.其中正确的是_____.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象的对称轴是直线x=2,且图象过点(1,2),与一次函数y=x+m的图象交于(0,-1).
(1)求两个函数解析式;
(2)求两个函数图象的另一个交点.
查看答案和解析>>
科目:初中数学 来源: 题型:
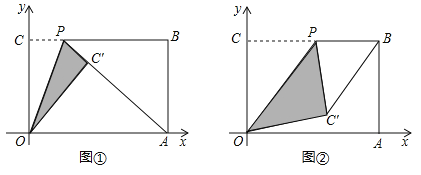
【题目】将一个矩形纸片![]() 放置在平面直角坐标系
放置在平面直角坐标系![]() 内,点
内,点![]() ,点
,点![]() ,点
,点![]() .点
.点![]() 是线段
是线段![]() 上的动点,将
上的动点,将![]() 沿
沿![]() 翻折得到
翻折得到![]() .
.
(Ⅰ)如图①,当点![]() 落在线段
落在线段![]() 上时,求点
上时,求点![]() 的坐标;
的坐标;
(Ⅱ)如图②,当点![]() 为线段
为线段![]() 中点时,求线段
中点时,求线段![]() 的长度;
的长度;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个矩形纸片OABC放置在平面直角坐标系xOy内,点A(6,0),点C(0,4),点O(0,0).点P是线段BC上的动点,将△OCP沿OP翻折得到△OC′P.
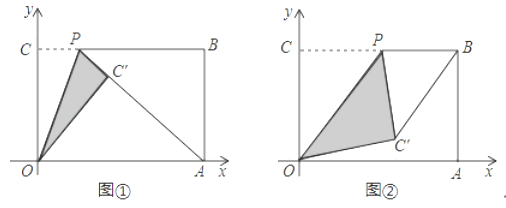
(Ⅰ)如图①,当点C′落在线段AP上时,求点P的坐标;
(Ⅱ)如图②,当点P为线段BC中点时,求线段BC′的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
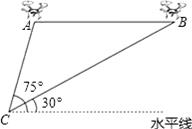
【题目】某兴趣小组借助无人飞机航拍校园.如图,无人飞机从A处水平飞行至B处需8秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中是抛物线拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为α、β,且tanα=![]() ,tanβ=
,tanβ=![]() ,以O为原点,OA所在直线为x轴建立直角坐标系.
,以O为原点,OA所在直线为x轴建立直角坐标系.
(1)求点P的坐标;
(2)水面上升1m,水面宽多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com