
【题目】如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q分别为AB、BC边上的动点,点P从点A开始沿AB方向运动,且速度为每秒1cm,点Q从点B开始B→C方向运动,且速度为每秒2cm,它们同时出发;设出发的时间为t秒.
(1)出发2秒后,求PQ的长;
(2)从出发几秒钟后,△PQB能形成等腰三角形?
(3)在运动过程中,直线PQ能否把原三角形周长分成相等的两部分?若能够,请求出运动时间;若不能够,请说明理由.

【答案】
【1】(1)出发2秒后,BP=6,BQ=4,PQ=![]() ;
;
【2】(2)设时间为t,列方程得
2t=8-1×t,
解得t=![]() ;
;
【3】(3)根据勾股定理可知AC=10cm,即三角形的周长为24cm,则有BP+BQ=12,
设时间为t,列方程得]
2t+(8-1×t)=12,
解得t=4,
当t=4时,点Q运动的路程是4×2=8>6,
所以不能够. ………………………………………………………(4分)
【解析】
(1)我们求出BP、BQ的长,用勾股定理解决即可.
(2)△PQB形成等腰三角形,即BP=BQ,我们可设时间为t,列出方程2t=8-1×t,解方程即得结果.
(3)直线PQ把原三角形周长分成相等的两部分,根据勾股定理可知AC=10cm,即三角形的周长为24cm,则有BP+BQ=12,即![]() 解方程即可
解方程即可
解:(1)出发2秒后,BP=6,BQ=4,PQ=![]() ;
;
(2)设时间为t,列方程得
2t=8-1×t,
解得t=![]() ;
;
(3)根据勾股定理可知AC=10cm,即三角形的周长为24cm,则有BP+BQ=12,
设时间为t,列方程得
![]()
解得t=4,
当t=4时,点Q运动的路程是4×2=8>6,
所以不能够.
本题重点考查了利用勾股定理解决问题的能力,综合性较强.


科目:初中数学 来源: 题型:
【题目】“校园手机”现象越来越受到社会的关注.小丽在“统计实习”活动中随机调查了学校若干名学生家长对“中学生带手机到学校”现象的看法,统计整理并制作了如下的统计图: 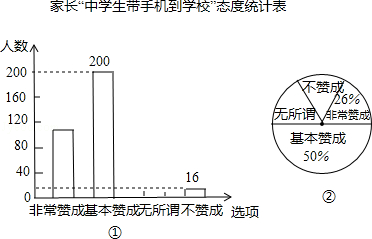
(1)求这次调查的家长总数及家长表示“无所谓”的人数,并补全图①;
(2)求图②中表示家长“无所谓”的圆心角的度数;
(3)从这次接受调查的家长中,随机抽查一个,恰好是“不赞成”态度的家长的概率是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据生物学研究结果,青春期男、女生身高增长速度呈现如下图规律,由图可以判断,下列说法错误的是( )
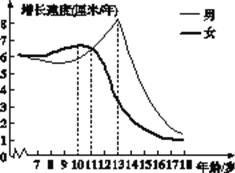
A. 男生在13岁时身高增长速度最快
B. 女生在10岁以后身高增长速度放慢
C. 11岁时男、女生身高增长速度基本相同
D. 女生身高增长的速度总比男生慢
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D为直线BC上一动点(点D不与B、C重合)以AD为边作正方形ADEF,使∠DAF=∠BAC,连接CF.
(1)如图1,当点D在线段BC上时,求证:BD=CF;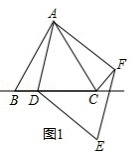
(2)如图2,当点D在线段BC的延长线上,且∠BAC=90°时.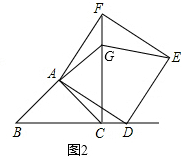
①问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
②延长BA交CF于点G,连接GE,若AB=2 ![]() ,CD=BC,请求出GE的长.
,CD=BC,请求出GE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB为⊙O的直径,⊙O与DC相切于点E,与AD相交于点F,已知AB=12,∠C=60°,则 ![]() 的长为( )
的长为( ) 
A.![]()
B.![]()
C.π
D.2π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海边的一段堤岸高出海平面12米,附近的某建筑物高出海平面50米,演习中的某潜水艇在海平面下30米处.
(1)现以海平面的高度为基准,将其记为0米,高于海平面记为正,低于海平面记为负,那么堤岸、附近建筑物及潜水艇的高度各应如何表示?
(2)若以堤岸高度为基准,则堤岸、建筑物及潜水艇的高度又应如何表示?

查看答案和解析>>
科目:初中数学 来源: 题型:
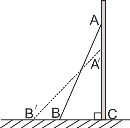
【题目】如图,一架2.5米长的梯子AB 斜靠在一座建筑物上,梯子底部与建筑物距离BC 为0.7米.
(1)求梯子上端A到建筑物的底端C的距离(即AC的长);
(2)如果梯子的顶端A沿建筑物的墙下滑0.4米(即AA′=0.4米),则梯脚B将外移(即BB′的长)多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA、PB是⊙O的切线,A、B是切点,点C是劣弧AB上的一个动点,若∠P=40°,则∠ACB的度数是( ) 
A.80°
B.110°
C.120°
D.140°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com