Question

17．若以正方形ABCD的一边CD为边作等边三角形△CDE，则∠BED=45或135°．

Answer 1

分析 解答本题时要考虑两种情况，E点在正方形内和外两种情况，由正方形和等边三角形的性质容易得出结果．

解答 解：分两种情况：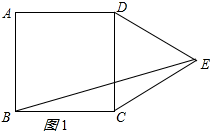
①当点E在正方形ABCD外侧时，如图1所示：
∵四边形ABCD是正方形，△CDE是等边三角形
∴∠BCD=90°，BC=CD=CE，∠DCE=∠CED=60°，
∴∠BCE=90°+60°=150°，
∵BC=CE，
∴∠CEB═∠CBE=15°，
∴∠BED=60°-15°=45°；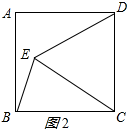
②当点E在正方形ABCD内侧时，如图2所示：
∵∠CED=∠DCE=60°，∠BCD=90°，
∴∠BCE=30°，
∵BC=CE，
∴∠BEC=∠EBC=75°，
∴∠BED=60°+75°=135°；
综上所述：∠BED为45°或135°；
故答案为：45或135．

点评 本题考查了正方形的性质、等边三角形的性质、钝角三角形的性质、三角形内角和定理等知识；熟练掌握正方形和等边三角形的性质，通过进行分类讨论得出结果是解题的关键