
【题目】直线![]() 是同一平面内的一组平行线.
是同一平面内的一组平行线.
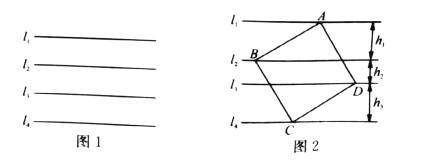
(1)如图1.正方形![]() 的4个顶点都在这些平行线上,若四条直线中相邻两条之间的距离都是1,其中点
的4个顶点都在这些平行线上,若四条直线中相邻两条之间的距离都是1,其中点![]() ,点
,点![]() 分别在直线
分别在直线![]() 和
和![]() 上,求正方形的面积;
上,求正方形的面积;
(2)如图2,正方形![]() 的4个顶点分别在四条平行线上,若四条直线中相邻两条之间的距离依次为
的4个顶点分别在四条平行线上,若四条直线中相邻两条之间的距离依次为![]() .
.
①求证:![]() ;
;
②设正方形![]() 的面积为
的面积为![]() ,求证
,求证![]() .
.
【答案】(1)9或5;(2)①见解析,②见解析
【解析】
(1)分两种情况:①如图1-1,得出正方形ABCD的边长为3,求出正方形ABCD的面积为9;
②如图1-2,过点B作EF⊥l1于E,交l4于F,则EF⊥l4,证明△ABE≌△BCF(AAS),得出AE=BF=2由勾股定理求出AB=![]() ,即可得出答案;
,即可得出答案;
(2)①过点B作EF⊥l1于E,交l4于F,作DM⊥l4于M,证明△ABE≌△BCF(AAS),得出AE=BF,同理△CDM≌△BCF(AAS),得出△ABE≌△CDM(AAS),得出BE=DM即可;
②由①得出AE=BF=h2+h3=h2+h1,得出正方形ABCD的面积S=AB2=AE2+BE2,即可得到答案.
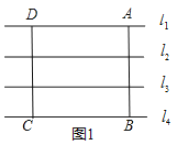
解:(1)①如图,当点![]() 分别在
分别在![]() 上时,面积为:
上时,面积为:![]() ;
;
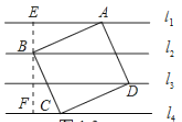
②如图,当点![]() 分别在
分别在![]() 上时,过点B作EF⊥l1于E,交l4于F,则EF⊥l4,
上时,过点B作EF⊥l1于E,交l4于F,则EF⊥l4,
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∴∠ABE+∠CBF=180°-90°=90°,
∵∠CBF+∠BCF=90°,
∴∠ABE=∠BCF,
在△ABE和△BCF中
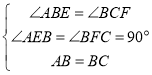 ,
,
∴△ABE≌△BCF(AAS),
∴AE=BF=2,
∴AB=![]() ,
,
∴正方形ABCD的面积=AB2=5;
综上所述,正方形ABCD的面积为9或5;
(2)①证明:过点B作EF⊥l1于E,交l4于F,作DM⊥l4于M,如图所示:则EF⊥l4,
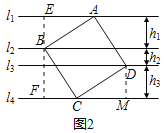
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∴∠ABE+∠CBF=180°-90°=90°,
∵∠CBF+∠BCF=90°,
∴∠ABE=∠BCF,
在△ABE和△BCF中,
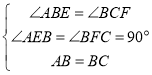 ,
,
∴△ABE≌△BCF(AAS),
∴AE=BF,
同理△CDM≌△BCF(AAS),
∴△ABE≌△CDM(AAS),
∴BE=DM,
即h1=h3.
②解:由①得:AE=BF=h2+h3=h2+h1,
∵正方形ABCD的面积:S=AB2=AE2+BE2,
∴S=(h2+h1)2+h12=2h12+2h1h2+h22.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ACBE内接于⊙O,AB平分∠CAE,CD⊥AB交AB、AE分别于点H、D.

(1)如图①,求证:BD=BE;
(2)如图②,若F是弧AC的中点,连接BF,交CD于点M,∠CMF=2∠CBF,连接FO、OC,求∠FOC的度数;
(3)在(2)的条件下,连接OD,若BC=4![]() ,OD=7,求BF的长.
,OD=7,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系xoy中,点M在x轴的正半轴上,⊙M交x轴于A、B两点,交y轴于C、D两点,且C为弧AE的中点,AE交y轴于G点,若点A的坐标为(-1,0),AE=4
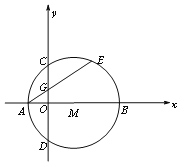
(1)求点C的坐标;
(2)连接MG、BC,求证:MG∥BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:关于x的二次函数![]() 的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
(1)求二次函数的表达式;
(2)在y轴上是否存在一点P,使△PBC为等腰三角形.若存在,请求出点P的坐标;
(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到 达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
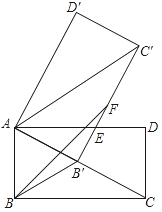
【题目】如图,矩形ABCD中,AC=2AB,将矩形ABCD绕点A旋转得到矩形AB′C′D′,使点B的对应点B'落在AC上,B'C'交AD于点E,在B'C′上取点F,使B'F=AB.
(1)求证:AE=C′E.
(2)求∠FBB'的度数.
(3)已知AB=2,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中不正确的是( )
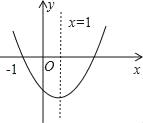
A. c<0
B. y的最小值为负值
C. 当x>1时,y随x的增大而减小
D. x=3是关于x的方程ax2+bx+c=0的一个根
查看答案和解析>>
科目:初中数学 来源: 题型:
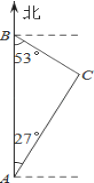
【题目】如图,禁渔期间,我渔政船在A处发现正北方向B处有一艘可疑船只,测得A、B两处距离为99海里,可疑船只正沿南偏东53°方向航行.我渔政船迅速沿北偏东27°方向前去拦截,2小时后刚好在C处将可疑船只拦截.求该可疑船只航行的速度.
(参考数据:sin27°≈![]() , cos27°≈
, cos27°≈![]() , tan27°≈
, tan27°≈![]() , sin53°≈
, sin53°≈![]() , cos53°≈
, cos53°≈![]() , tan53°≈
, tan53°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
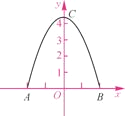
【题目】某工厂大门是一抛物线水泥建筑物(如图),大门地面宽AB=4 m,顶部C离地面高为4.4 m.
(1)以AB所在直线为x轴,抛物线的对称轴为y轴,建立平面直角坐标系,求该抛物线对应的函数表达式;
(2)现有一辆载满货物的汽车欲通过大门,货物顶点距地面2.8 m,装货宽度为2.4 m,请通过计算,判断这辆汽车能否顺利通过大门.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】动物学家通过大量的调查估计出,某种动物活到20岁的概率为0.8,活到25岁的概率是0.5,活到30岁的概率是0.3.现年20岁的这种动物活到25岁的概率为多少?现年25岁的这种动物活到30岁的概率为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com