
分析 分①以AC=5为轴旋转一周和②以BC=12为轴旋转一周两种情况,先得出圆锥的底面圆的半径及母线长,根据S=$\frac{1}{2}$•2πr•L可得答案.
解答 解:①若以AC=5为轴旋转一周,
则圆锥的底面半径为BC=12,母线AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=13,
∴斜边AB形成的圆锥的侧面积为$\frac{1}{2}$×2π×12×13=156π;
②若以BC=12为轴旋转一周,
则圆锥的底面半径为AC=5,母线AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=13,
∴斜边AB形成的圆锥的侧面积为$\frac{1}{2}$×2π×5×13=65π.
点评 本题主要考查圆锥的计算、勾股定理及旋转体,根据题意分类讨论得出旋转所得几何体的底面圆的半径及母线长是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从A向B以2cm/s的速度移动;点Q沿DA边从D向A以1cm/s的速度移动.如果P,Q同时出发,用t(s)表示移动时间(0≤t≤6),那么:
如图,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从A向B以2cm/s的速度移动;点Q沿DA边从D向A以1cm/s的速度移动.如果P,Q同时出发,用t(s)表示移动时间(0≤t≤6),那么:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
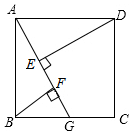 已知:在正方形ABCD中,点G是BC边上的任意一点,DE⊥AG于点E,BF∥DE,交AG于点F. 求证:
已知:在正方形ABCD中,点G是BC边上的任意一点,DE⊥AG于点E,BF∥DE,交AG于点F. 求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com