
【题目】(1)一个凸多边形除一个内角外,其余各角之和为2750°,这个多边形的边数为__________,除去的这个内角的度数为__________.
(2)一个多边形截去一个角后,形成另一个多边形的内角和是1620°,则原来多边形的边数是____.
(3)一个凸多边形的某一个内角的外角与其余内角的和恰为500°,那么这个多边形的边数是_____.
【答案】18 130° 10,11,12 4或5
【解析】
(1)设这个多边形的边数为a,根据凸多边形的内角和公式列出不等式,再根据a的整数性可得出a的值,从而可得内角和,然后减去![]() 即可得出答案;
即可得出答案;
(2)先根据内角和公式求出剪完后多边形的边数,从而可得原来多边形的边数;
(3)设这个多边形的边数为![]() ,这个内角的度数为x,先根据内角和公式、外角的定义列出等式,求出n的等式,再根据n为正整数、
,这个内角的度数为x,先根据内角和公式、外角的定义列出等式,求出n的等式,再根据n为正整数、![]() 求解即可.
求解即可.
(1)设这个多边形的边数为![]() ,则这个多边形的内角和为
,则这个多边形的内角和为![]()
由题意得![]()
解得![]()
因a为正整数
则![]() ,除去的这个内角的度数为
,除去的这个内角的度数为![]()
故答案为:18;![]() ;
;
(2)设剪去一个角后,形成的多边形的边数为![]()
则![]()
解得![]()
因为一个多边形截去一个角后,其边数可以增加1条、不变、减少1条
所以原来多边形的边数为10或11或12
故答案为:10或11或12;
(3)设这个多边形的边数为![]() ,这个内角的度数为x
,这个内角的度数为x
由题意得![]()
解得![]()
![]() 为正整数
为正整数
![]() 是
是![]() 的倍数
的倍数
又![]() ,即有
,即有![]()
![]() 或
或![]()
代入![]() ,解得
,解得![]() 或5
或5
故答案为:4或5.


科目:初中数学 来源: 题型:
【题目】小强在做课后习题时,遇到这样一道题:“如图所示,![]() 、
、![]() 两村庄在一条河的两岸,从
两村庄在一条河的两岸,从![]() 村庄去
村庄去![]() 村庄,需要在河上造一座桥
村庄,需要在河上造一座桥![]() ,请问桥造在何处从
,请问桥造在何处从![]() 村庄去
村庄去![]() 村庄的路径最短?(假定河的两岸是平行的直线,桥与河垂直)”
村庄的路径最短?(假定河的两岸是平行的直线,桥与河垂直)”
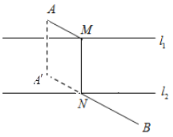
小强的解题思路,因为桥与河岸垂直,线段![]() 是一个不变的量,将它平移到
是一个不变的量,将它平移到![]() 处得线段
处得线段![]() ,总的路程
,总的路程![]() 与
与![]() 是相等的,故要使
是相等的,故要使![]() 最短,就是求点
最短,就是求点![]() 到点
到点![]() 最短即可,所以点
最短即可,所以点![]() 应是
应是![]() 与
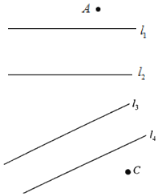
与![]() 的交点.根据上述材料解答下列问题:如图所示:
的交点.根据上述材料解答下列问题:如图所示:![]() 、
、![]() 两个驻军地被两条河隔开,上级安排紧急任务,现要求一名士兵从
两个驻军地被两条河隔开,上级安排紧急任务,现要求一名士兵从![]() 地出发到
地出发到![]() 地完成这项任务,现要修两座与河岸垂直的桥,问桥建在何处使得这名士兵走的路径最短?(假定河的两岸是平行的直线,河
地完成这项任务,现要修两座与河岸垂直的桥,问桥建在何处使得这名士兵走的路径最短?(假定河的两岸是平行的直线,河![]() 与
与![]() 的宽为
的宽为![]() ,河
,河![]() 与
与![]() 的宽为
的宽为![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 经过点A(
经过点A(![]() ,0),B(
,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
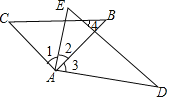
【题目】若将一副三角板按如图所示的方式放置,则下列结论:①![]() ;②如果
;②如果![]() ,则有
,则有![]() ;③如果
;③如果![]() ,则有
,则有![]() ;④如果
;④如果![]() ,必有
,必有![]() ;其中正确的有( )
;其中正确的有( )
A.①②③B.①②④C.②③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
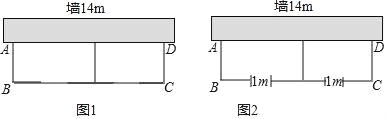
【题目】如图,有长为22米的篱笆,一面利用墙(墙的最大可用长度为14米),围成中间隔有一道篱笆的长方形花圃,有以下两种围法.
(1)如图1,设花圃的宽AB为x米,面积为y米2,求y与x之间的含函数表达式,并确定x的取值范围;
(2)如图2,为了方便出入,在建造篱笆花圃时,在BC上用其他材料造了宽为1米的两个小门,设花圃的宽AB为a米,面积为S米2,求S与a之间的函数表达式及S的最大值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,六边形 ABCDEF 中,∠A+∠B+∠C=∠D+∠E+∠F,猜想可 得六边形 ABCDEF 中必有两条边是平行的.

(1)根据图形写出你的猜想: ∥ ;
(2)请证明你在(1)中写出的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
“ a 2 ≥0”这个结论在数学中非常有用,有时我们需要将代数式配成完全平方式.例如:
x2 4x 5 x2 4x 4 1 x 22 1 ,
∵ x 22 ≥0,
∴ x 22 1 ≥1,
∴ x2 4x 5 ≥1.
试利用“配方法”解决下列问题:
(1)填空: x2 4x 5 ( x )2+ ;
(2)已知 x2 4x y2 2y 5 0 ,求 x y 的值;
(3)比较代数式 x2 1与2x 3 的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD 中,点E,O,F分别是边AB,AC,AD的中点,连接CE、CF、OE、OF.
(1)求证:△BCE≌△DCF;
(2)当AB与BC满足什么条件时,四边形AEOF正方形?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com