
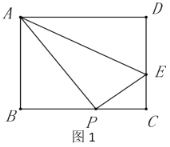
【题目】如图1,已知在矩形![]() 中,
中,![]() ,
,![]() 是
是![]() 上一点,且
上一点,且![]() ,点
,点![]() 是
是![]() 上一点,
上一点,![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)求![]() 的长;
的长;
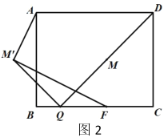
(3)如图2,点![]() 在
在![]() 边上且
边上且![]() ,点
,点![]() 是边
是边![]() 上的一动点,且从点
上的一动点,且从点![]() 向点
向点![]() 方向运动.连接
方向运动.连接![]() ,
,![]() 是
是![]() 的中点,将点
的中点,将点![]() 绕点
绕点![]() 逆时针旋转90°,点
逆时针旋转90°,点![]() 的对应点是
的对应点是![]() ,在点
,在点![]() 的运动过程中,①判断
的运动过程中,①判断![]() 是否为定值?若是说明理由.②求
是否为定值?若是说明理由.②求![]() 的最小值.
的最小值.
【答案】(1)证明见解析;(2)![]() ;(3)①不变,见解析,②
;(3)①不变,见解析,②![]()
【解析】
(1)由SAS证明△APE≌△ADE得出∠APE=∠D=90°即可;
(2)由全等三角形的性质得出PE=DE=5,设BP=x,则PC=10x,证明△ABP∽△PCE,得出![]() ,得出AB=202x,CE=
,得出AB=202x,CE=![]() x,由AB=CD得出方程,解方程即可得出结果;
x,由AB=CD得出方程,解方程即可得出结果;
(3)①作MG⊥B于G,M'H⊥BC于H,证明△HQM'≌△GMQ得出HM'=GQ,QH=MG=4,设HM'=x,则CG=GQ=x,FG=4x,求出QF=GQFG=2x4,得出FH=QH+QF=2x,由三角函数得出tan∠∠M′FB=![]() ,即可得出结论;
,即可得出结论;
②当AM'⊥FM'时,AM'的值最小,延长HM'交DA延长线于N,则NH=AB=8,NM'=8x,AN=BH=HQBQ=2x6,同①得:△ANM'∽△M'HF,得出![]() ,解得:x=4,得出AN=2,NM'=4,在Rt△ANM'中,由勾股定理即可得出结果.
,解得:x=4,得出AN=2,NM'=4,在Rt△ANM'中,由勾股定理即可得出结果.
(1)证明:∵四边形ABCD是矩形,
∴BC=AD=10,AB=CD,∠B=∠C=∠D=90°,
∵AD=10,PA=10,∠PAD=2∠DAE,
∴AP=AD,∠PAE=∠DAE,
在△APE和△ADE中,
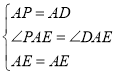 ,
,
∴△APE≌△ADE(SAS),
∴∠APE=∠D=90°;
(2)解:由(1)得:△APE≌△ADE,
∴PE=DE=5,
设BP=x,则PC=10x,
∵∠B=90°,∠APE=90°,
∴∠BAP+∠APB=90°,∠APB+∠CPE=90°,
∴∠BAP=∠CPE,
∴△ABP∽△PCE,
∴![]() ,即
,即![]() =2,
=2,
∴AB=202x,CE=![]() x,
x,
∵AB=CD,
∴202x=5+![]() x,
x,
解得:x=6,
∴AB=202x=8;
(3)解:①∠M′FB为定值,理由如下:
作MG⊥B于G,M'H⊥BC于H,如图2所示:
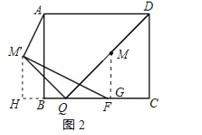
则MG∥CD,∠H=∠MGQ=90°,
∴∠QMG+∠MQG=90°,
∵M是DQ的中点,
∴QG=CG,
∴MG是△CDQ的中位线,
∴MG=![]() CD=
CD=![]() AB=4,
AB=4,
由旋转的性质,QM'=QM,∠M'QM=90°,
∴∠HQM'+∠MQG=90°,
∴∠HQM'=∠QMG,
在△HQM'和△GMQ中,
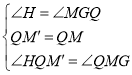 ,
,
∴△HQM'≌△GMQ(ASA),
∴HM'=GQ,QH=MG=4,
设HM'=x,则CG=GQ=x,
∴FG=4x,
∴QF=GQFG=2x(4x)=2x4,
∴FH=QH+QF=2x,
∴tan∠M′FB=![]() ,
,
∴∠M′FB为定值;
②当AM'⊥FM'时,AM'的值最小,延长HM'交DA延长线于N,如图3所示:
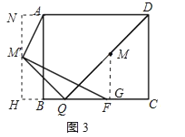
则NH=AB=8,NM'=8x,AN=BH=HQBQ=4(102x)=2x6,
同①得:△ANM'∽△M'HF,
∴![]() ,
,
∴![]() ,
,
解得:x=4,
∴AN=2,NM'=4,
在Rt△ANM'中,由勾股定理得:AM'=![]() .
.


科目:初中数学 来源: 题型:
【题目】近年,《中国诗词大会》、《朗读者》,《经典咏流传》、《国家宝藏》等文化类节目相继走红,被人们称为“清流综艺”,六中上智中学某兴趣小组想了解全校学生对这四个节目的喜爱情况,随机抽取了部分学生进行调查统计,要求每名学生选出一个自己最喜爱的节目,并将调查结果给制成如下统计图(其中《中国诗词大会》,《朗读者》,《经典咏流传》,《国家宝藏》分别用A,B,C.D表示),请你结合图中信息解答下列问题:
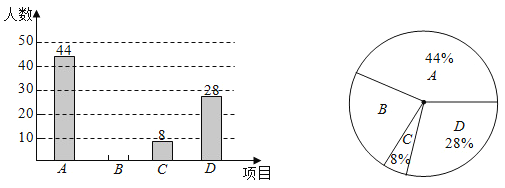
(1)本次调查的学生人数是 人:
(2)请把条形统计图补充完整.
(3)在扇形统计图中,B对应的圆心角的度数是 .
(4)已知六中上智中学共有3200名学生,请根据样本估计全校最喜爱《朗读者》的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某省对部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,![]() 级:对学习很感兴趣;
级:对学习很感兴趣;![]() 级:对学习较感兴趣;
级:对学习较感兴趣;![]() 级:对学习不感兴趣),并将调查结果绘制成图①和图②不完整的统计图.请根据图中提供的信息,解答下列问题:
级:对学习不感兴趣),并将调查结果绘制成图①和图②不完整的统计图.请根据图中提供的信息,解答下列问题:
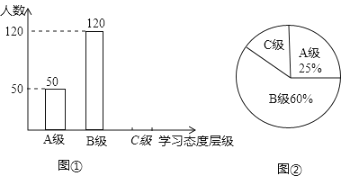
(1)此次抽样调查中,共调查了______名学生;
(2)将图①补充完整;
(3)求出图②中![]() 级所占的圆心角的度数;
级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计该省近40000名八年级学生中大约有多少名学生学习态度达标(达标包括![]() 级和
级和![]() 级)?
级)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应国家的“一带一路”经济发展战略,树立品牌意识,我市质检部门对![]() ,
,![]() ,
,![]() ,
,![]() 四个厂家生产的同种型号的零件共2000件进行合格率检测,通过检测得出
四个厂家生产的同种型号的零件共2000件进行合格率检测,通过检测得出![]() 厂家的合格率为
厂家的合格率为![]() ,并根据检测数据绘制了两幅不完整的统计图.
,并根据检测数据绘制了两幅不完整的统计图.
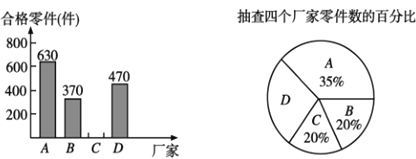
(1)抽查![]() 厂家的零件为______件,扇形统计图中
厂家的零件为______件,扇形统计图中![]() 厂家对应的圆心角为______.
厂家对应的圆心角为______.
(2)抽查![]() 厂家的合格零件为_______件.
厂家的合格零件为_______件.
(3)若要从![]() ,
,![]() ,
,![]() ,
,![]() 四个厂家中,随机抽取两个厂家参加德国工业产品博览会,请用列表法或画树状图的方法求出
四个厂家中,随机抽取两个厂家参加德国工业产品博览会,请用列表法或画树状图的方法求出![]() ,
,![]() 两个厂家同时被选中的概率,并列出所有等可能的结果.
两个厂家同时被选中的概率,并列出所有等可能的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y![]() x2沿x轴正方向平移后经过点A(x1,y2),B(x2,y2),其中x1,x2是方程x2﹣2x=0的两根,且x1>x2,
x2沿x轴正方向平移后经过点A(x1,y2),B(x2,y2),其中x1,x2是方程x2﹣2x=0的两根,且x1>x2,
(1)如图.求A,B两点的坐标及平移后抛物线的解析式;
(2)平移直线AB交抛物线于M,交x轴于N,且![]() ,求△MNO的面积;
,求△MNO的面积;
(3)如图,点C为抛物线对称轴上顶点下方的一点,过点C作直线交抛物线于E、F,交x轴于点D,探究![]() 的值是否为定值?如果是,求出其值;如果不是,请说明理由.
的值是否为定值?如果是,求出其值;如果不是,请说明理由.
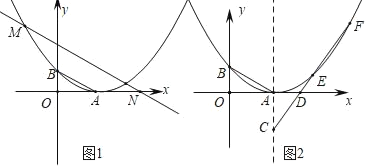
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】太阳能是来自太阳的辐射能量,对于地球上的人类来说,太阳能是对环境无任何污染的可再生能源,因此许多国家都在大陆发展太阳能.如图是2013-2017年我国光伏发电装机容量统计图.根据统计图提供的信息,判断下列说法不合理的是( )
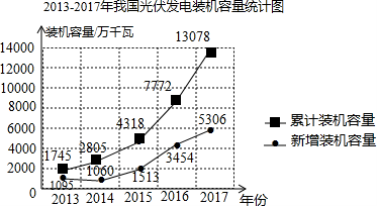
A.截至2017年底,我国光伏发电累计装机容量为13078万千瓦
B.2013-2017年,我国光伏发电新增装机容量逐年增加
C.2013-2017年,我国光伏发电新增装机容量的平均值约为2500万千瓦
D.2017年我国光伏发电新增装机容量大约占当年累计装机容量的40%
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com