
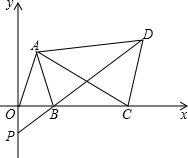
 如图,平面直角坐标系中,已知点A(1,3),B (2,0),C为x轴上点B右侧的动点,以AC为腰作等腰△ACD,使AD=AC,∠CAD=∠OAB,直线DB交y轴于点P.
如图,平面直角坐标系中,已知点A(1,3),B (2,0),C为x轴上点B右侧的动点,以AC为腰作等腰△ACD,使AD=AC,∠CAD=∠OAB,直线DB交y轴于点P.分析 (1)作AE⊥OB于点E,由SAS定理得出△AEO≌△AEB,根据全等三角形的性质即可得出结论;
(2)先根据∠CAD=∠OAB,得出∠OAC=∠BAD,再由SAS定理即可得出△AEO≌△AEB;
(3)设∠AOB=∠ABO=α,由全等三角形的性质可得出∠ABD=∠AOB=α,故∠OBP=180°-∠ABO-∠ABD=180°-2α为定值,再由OB=2,∠POB=90°可知OP的长度不变,故可得出结论.
解答 解:(1)如图,作AE⊥OB于点E,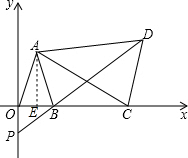
∵A(1,3),B(2,0),
∴OE=1,BE=2-1=1,
∴OE=BE,
在△AEO与△AEB中,
∵$\left\{\begin{array}{l}{AE=AE}\\{∠AEO=∠AEB=90°}\\{OE=BE}\end{array}\right.$,
∴△AEO≌△AEB,
∴AO=AB;
(2)∵∠CAD=∠OAB,
∴∠CAD+∠BAC=∠OAB+∠BAC,即∠OAC=∠BAD,
在△AOC与△ABD中,
∵$\left\{\begin{array}{l}{OA=AB}\\{∠OAC=∠BAD}\\{AC=AD}\end{array}\right.$,
∴△AOC≌△ABD(SAS);
(3)当∠ACO=30°时,AD=6;
点P在y轴上的位置不发生改变.
理由:设∠AOB=∠ABO=α,
∵由(2)知,△AOC≌△ABD,
∴∠ABD=∠AOB=α,
∵OB=2,∠OBP=180°-∠ABO-∠ABD=180°-2α为定值,∠POB=90°,
∴OP长度不变.
故答案为:6.
点评 本题考查的是全等三角形的判定与性质,熟知全等三角形的判定定理是解答此题的关键.


科目:初中数学 来源: 题型:选择题
 如图,BC是⊙O的直径,点D在⊙O上,AB是⊙O的切线,B为切点,连接CD并延长交AB于点A,若∠BOD=100°,则∠BAC的度数是( )
如图,BC是⊙O的直径,点D在⊙O上,AB是⊙O的切线,B为切点,连接CD并延长交AB于点A,若∠BOD=100°,则∠BAC的度数是( )| A. | 40° | B. | 45° | C. | 50° | D. | 80° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
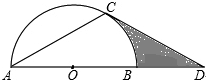 如图,AC是⊙O的弦,AD经过圆心O,交⊙O于点B,直线CD与⊙O相切,∠CAD=30°.
如图,AC是⊙O的弦,AD经过圆心O,交⊙O于点B,直线CD与⊙O相切,∠CAD=30°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com