
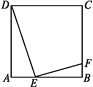
【题目】如图,在四边形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上一点,
边上一点,![]() ,
,![]() ,垂足为点
,垂足为点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
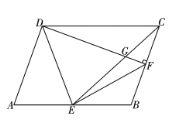
(1)四边形![]() 是平行四边形吗?说明理由;
是平行四边形吗?说明理由;
(2)求证:![]() ;
;
(3)若点![]() 是
是![]() 边的中点,求证:
边的中点,求证:![]() .
.
【答案】(1)四边形![]() 是平行四边形,理由见解析;(2)见解析;(3)见解析
是平行四边形,理由见解析;(2)见解析;(3)见解析
【解析】
(1)由![]() 可得AB∥DC,再由AB=DC即可判定四边形ABCD为平行四边形;
可得AB∥DC,再由AB=DC即可判定四边形ABCD为平行四边形;
(2)由AB∥DC可得∠AED=∠CDE,然后根据CE=AB=DC可得∠CDE=∠CED,再利用三角形内角和定理即可推出∠AED与∠DCE的关系;
(3)延长DA,FE交于点M,由“AAS”可证△AEM≌△BEF,可得ME=EF,由直角三角形的性质可得DE=EF=ME,由等腰三角形的性质和外角性质可得结论.
(1)四边形![]() 是平行四边形,理由如下:
是平行四边形,理由如下:
∵![]()
∴AB∥DC
又∵AB=DC
∴四边形![]() 是平行四边形.
是平行四边形.
(2)∵AB∥DC
∴∠AED=∠CDE
又∵AB=DC,CE=AB
∴DC=CE
∴∠CDE=∠CED
∴在△CDE中,2∠CDE+∠DCE=180°
∴∠CDE=90°-![]() ∠DCE
∠DCE
∴![]()
(3)如图,延长DA,FE交于点M,
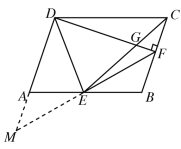
∵四边形ABCD为平行四边形
∴DM∥BC,DF⊥BC
∴∠M=∠EFB,DF⊥DM
∵E为AB的中点
∴AE=BE
在△AEM和△BEF中,
∵∠M=∠EFB,∠AEM=∠BEF,AE=BE
∴△AEM≌△BEF(AAS)
∴ME=EF
∴在Rt△DMF中,DE为斜边MF上的中线
∴DE=ME=EF
∴∠M=∠MDE,
∴∠DEF=∠M+∠MDE=2∠M=2∠EFB.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过边长为3的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为_____.
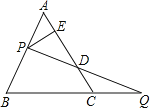
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,李老师出示了如下框中的题目.
在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,如图.试确定线段AE与DB的大小关系,并说明理由. |
|
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:
AE DB(填“>”,“<”或“=”).

图1 图2
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”).
理由如下:如图2,过点E作EF∥BC,交AC于点F.
(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长(请你直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB=4,AD=5,tanA=![]() ,点P从点A出发,沿折线AB﹣BC以每秒1个单位长度的速度向中点C运动,过点P作PQ⊥AB,交折线AD﹣DC于点Q,将线段PQ绕点P顺时针旋转90°,得到线段PR,连接QR.设△PQR与ABCD重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).
,点P从点A出发,沿折线AB﹣BC以每秒1个单位长度的速度向中点C运动,过点P作PQ⊥AB,交折线AD﹣DC于点Q,将线段PQ绕点P顺时针旋转90°,得到线段PR,连接QR.设△PQR与ABCD重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).
(1)当点R与点B重合时,求t的值;
(2)当点P在BC边上运动时,求线段PQ的长(用含有t的代数式表示);
(3)当点R落在ABCD的外部时,求S与t的函数关系式;
(4)直接写出点P运动过程中,△PCD是等腰三角形时所有的t值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,点![]() 是等边
是等边![]() 内一点,
内一点,![]() ,
,![]() .以
.以![]() 为边作等边三角形
为边作等边三角形![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
(2)当![]() 时(如图②),试判断
时(如图②),试判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)求当![]() 是多少度时,
是多少度时,![]() 是等腰三角形?(写出过程)
是等腰三角形?(写出过程)
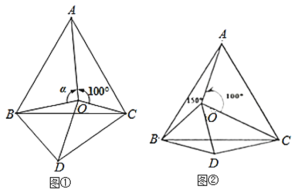
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,P,B,C是半径为8的⊙O上的四点,且满足∠BAC=∠APC=60°,

(1)求证:△ABC是等边三角形;
(2)求圆心O到BC的距离OD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是正方形ABCD的边AB上的动点,EF⊥DE交BC于点F.
(1)求证:△ADE∽△BEF.
(2)设正方形的边长为4,AE=x,BF=y.当x取什么值时,y有最大值?并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”,随着生活水平的提高人们对饮水品质的需求越来越高,岳阳市槐荫公司根据市场需求代理![]() ,
,![]() 两种型号的净水器,每台
两种型号的净水器,每台![]() 型净水器比每台
型净水器比每台![]() 型净水器进价多
型净水器进价多![]() 元,用
元,用![]() 万元购进
万元购进![]() 型净水器与用
型净水器与用![]() 万元购进
万元购进![]() 型净水器的数量相等
型净水器的数量相等
(1)求每台![]() 型、
型、![]() 型净水器的进价各是多少元?
型净水器的进价各是多少元?
(2)槐荫公司计划购进![]() ,
,![]() 两种型号的共
两种型号的共![]() 台进行试销,,购买资金不超过
台进行试销,,购买资金不超过![]() 万元.试求最多可以购买
万元.试求最多可以购买![]() 型净水器多少台?
型净水器多少台?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com