
【题目】如图,在ABCD中,AB=4,AD=5,tanA=![]() ,点P从点A出发,沿折线AB﹣BC以每秒1个单位长度的速度向中点C运动,过点P作PQ⊥AB,交折线AD﹣DC于点Q,将线段PQ绕点P顺时针旋转90°,得到线段PR,连接QR.设△PQR与ABCD重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).
,点P从点A出发,沿折线AB﹣BC以每秒1个单位长度的速度向中点C运动,过点P作PQ⊥AB,交折线AD﹣DC于点Q,将线段PQ绕点P顺时针旋转90°,得到线段PR,连接QR.设△PQR与ABCD重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).
(1)当点R与点B重合时,求t的值;
(2)当点P在BC边上运动时,求线段PQ的长(用含有t的代数式表示);
(3)当点R落在ABCD的外部时,求S与t的函数关系式;
(4)直接写出点P运动过程中,△PCD是等腰三角形时所有的t值.

【答案】(1)![]() ;(2)
;(2)![]() (9﹣t);(3)①S =﹣
(9﹣t);(3)①S =﹣![]() t2+
t2+![]() t﹣
t﹣![]() ;②S=﹣
;②S=﹣![]() t2+8.③S=
t2+8.③S=![]() (9﹣t)2;(4)4或
(9﹣t)2;(4)4或![]() 或5或
或5或![]() .
.
【解析】
(1)根据题意点R与点B重合时t+![]() t=4,即可求出t的值;
t=4,即可求出t的值;
(2)根据题意运用t表示出PQ即可;
(3)当点R落在□ABCD的外部时可得出t的取值范围,再根据等量关系列出函数关系式;
(4)根据等腰三角形的性质即可得出结论.
解:(1)∵将线段PQ绕点P顺时针旋转90°,得到线段PR,
∴PQ=PR,∠QPR=90°,
∴△QPR为等腰直角三角形.
当运动时间为t秒时,AP=t,PQ=PQ=APtanA=![]() t.
t.
∵点R与点B重合,
∴AP+PR=t+![]() t=AB=4,
t=AB=4,
解得:t=![]() .
.
(2)当点P在BC边上时,4≤t≤9,CP=9﹣t,
∵tanA=![]() ,
,
∴tanC=![]() ,sinC=
,sinC=![]() ,
,
∴PQ=CPsinC=![]() (9﹣t).
(9﹣t).
(3)①如图1中,当![]() <t≤3时,重叠部分是四边形PQKB.作KM⊥AR于M.
<t≤3时,重叠部分是四边形PQKB.作KM⊥AR于M.
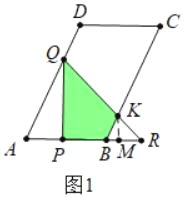
∵△KBR∽△QAR,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴KM=![]() (
(![]() t﹣4)=
t﹣4)=![]() t﹣
t﹣![]() ,
,
∴S=S△PQR﹣S△KBR=![]() ×(
×(![]() t)2﹣
t)2﹣![]() ×(
×(![]() t﹣4)(
t﹣4)(![]() t﹣
t﹣![]() )=﹣
)=﹣![]() t2+
t2+![]() t﹣
t﹣![]() .
.
②如图2中,当3<t≤4时,重叠部分是四边形PQKB.
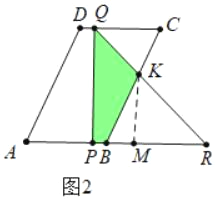
S=S△PQR﹣S△KBR=![]() ×4×4﹣
×4×4﹣![]() ×t×
×t×![]() t=﹣
t=﹣![]() t2+8.
t2+8.
③如图3中,当4<t<9时,重叠部分是△PQK.
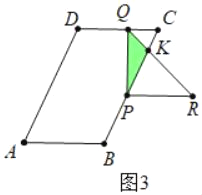
S=![]() S△PQC=
S△PQC=![]() ×
×![]() ×
×![]() (9﹣t)
(9﹣t)![]() (9﹣t)=
(9﹣t)=![]() (9﹣t)2.
(9﹣t)2.
(4)如图4中,
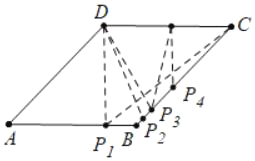
①当DC=DP1=4时,易知AP1=4,t=4.
②当DC=DP2时,CP2=2CD![]() =
=![]() ,
,
∴BP2=![]() ,
,
∴t=4+![]() =
=![]() .
.
③当CD=CP3时,t=5.
④当CP4=DP4时,CP4=2÷![]() =
=![]() ,
,
∴t=9﹣![]() =
=![]() .
.
综上所述,满足条件的t的值为4或![]() 或5或
或5或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE相交于点O,给出四个条件:①OB=OC;②∠EBO=∠DCO;③∠BEO=∠CDO;④BE=CD.上述四个条件中,选择两个可以判定△ABC是等腰三角形的方法有( )
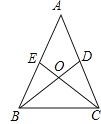
A.2种B.3种C.4种D.6种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有4张正面分别标有数字﹣1,2,﹣3,4的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上,洗匀后从4张卡片中随机摸出一张不放回,将该卡片上的数字记为m,在随机抽取1张,将卡片的数字即为n.
(1)请用列表或树状图的方式把(m,n)所有的结果表示出来.
(2)求选出的(m,n)在二、四象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(a)所示点D是等边![]() 边BA上一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边
边BA上一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边![]() ,连接AF.你能发现线段AF与BD之间的数量关系吗?并证明.
,连接AF.你能发现线段AF与BD之间的数量关系吗?并证明.
(2)如图(b)所示当动点D运动至等边![]() 边BA的延长线上时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是否仍然成立?(直接写出结论)
边BA的延长线上时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是否仍然成立?(直接写出结论)
(3)①如图(c)所示,当动点D在等边![]() 边BA上运动时(点D与点B不重合),连接DC,以DC为边在BC上方、下方分别作等边
边BA上运动时(点D与点B不重合),连接DC,以DC为边在BC上方、下方分别作等边![]() 和等边
和等边![]() ,连接AF、
,连接AF、![]() ,探究AF、
,探究AF、![]() 与AB有何数量关系?并证明.
与AB有何数量关系?并证明.
②如图(d)所示,当动点D在等边![]() 边BA的延长线上运动时,其他作法与(3)①相同,①中的结论是否成立?若不成立,是否有新的结论?并证明.
边BA的延长线上运动时,其他作法与(3)①相同,①中的结论是否成立?若不成立,是否有新的结论?并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上一点,
边上一点,![]() ,
,![]() ,垂足为点
,垂足为点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
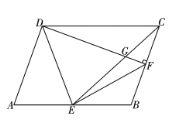
(1)四边形![]() 是平行四边形吗?说明理由;
是平行四边形吗?说明理由;
(2)求证:![]() ;
;
(3)若点![]() 是
是![]() 边的中点,求证:
边的中点,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在![]() 中,
中,![]() ,
,![]() ,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N再分别以MN为圆心,大于
,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N再分别以MN为圆心,大于![]() 的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法中正确的有________.
的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法中正确的有________.
①AD是![]() 的平分线;②
的平分线;②![]() ;③点D在AB的中垂线上;④
;③点D在AB的中垂线上;④![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
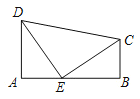
【题目】如图,四边形![]() 中,
中,![]() .动点
.动点![]() 从
从![]() 点出发,以
点出发,以![]() 的速度向
的速度向![]() 点移动,设移动的时间为
点移动,设移动的时间为![]() 秒.
秒.
(1)当![]() 为何值时,点
为何值时,点![]() 在线段
在线段![]() 的垂直平分线上?
的垂直平分线上?
(2)在(1)的条件下,判断![]() 与
与![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点A在半径为20的圆O上,以OA为一条对角线作矩形OBAC,设直线BC交圆O于D、E两点,若OC=12,则线段CE、BD的长度差是_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com