
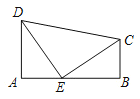
【题目】如图,四边形![]() 中,
中,![]() .动点
.动点![]() 从
从![]() 点出发,以
点出发,以![]() 的速度向
的速度向![]() 点移动,设移动的时间为
点移动,设移动的时间为![]() 秒.
秒.
(1)当![]() 为何值时,点
为何值时,点![]() 在线段
在线段![]() 的垂直平分线上?
的垂直平分线上?
(2)在(1)的条件下,判断![]() 与
与![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
【答案】(1)当x=5时,点E在线段CD的垂直平分线上;(2)DE与CE的位置关系是DE⊥CE,理由见解析
【解析】
(1)根据垂直平分线的性质得出DE=CE,利用勾股定理得出![]() ,然后建立方程求解即可
,然后建立方程求解即可
(2)根据第(1)问的结果,易证△ADE≌△BEC,根据全等三角形的性质有∠ADE=∠CEB,再通过等量代换可得∠AED+∠CEB=90°,进而求出∠DEC=90°,则可说明DE⊥CE.
解:(1) ∵点E在线段CD的垂直平分线上,
∴DE=CE,
∵∠A=∠B= 90°
![]()
![]()
![]()
![]()
解得![]()
∴当x=5时,点E在线段CD的垂直平分线上
(2)DE与CE的位置关系是DE⊥CE;
理由是:当x=5时,AE=2×5cm=10cm=BC,
∵AB=25cm,DA=15cm,CB=10cm,
∴BE=AD=15cm,
在△ADE和△BEC中,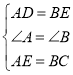
∴△ADE≌△BEC(SAS),
∴∠ADE=∠CEB,
∵∠A=90°,
∴∠ADE+∠AED=90°,
∴∠AED+∠CEB=90°,
∴∠DEC=180°-(∠AED+∠CEB)=90°,
∴DE⊥CE.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
【题目】“垃圾不落地,城市更美丽”.某中学为了了解七年级学生对这一倡议的落实情况,学校安排政教处在七年级学生中随机抽取了部分学生,并针对学生“是否随手丢垃圾”这一情况进行了问卷调查,统计结果为:A为从不随手丢垃圾;B为偶尔随手丢垃圾;C为经常随手丢垃圾三项.要求每位被调查的学生必须从以上三项中选一项且只能选一项.现将调查结果绘制成以下来不辜负不完整的统计图.
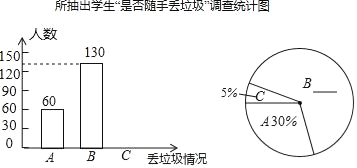
请你根据以上信息,解答下列问题:
(1)补全上面的条形统计图和扇形统计图;
(2)所抽取学生“是否随手丢垃圾”情况的众数是 ;
(3)若该校七年级共有1500名学生,请你估计该年级学生中“经常随手丢垃圾”的学生约有多少人?谈谈你的看法?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB=4,AD=5,tanA=![]() ,点P从点A出发,沿折线AB﹣BC以每秒1个单位长度的速度向中点C运动,过点P作PQ⊥AB,交折线AD﹣DC于点Q,将线段PQ绕点P顺时针旋转90°,得到线段PR,连接QR.设△PQR与ABCD重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).
,点P从点A出发,沿折线AB﹣BC以每秒1个单位长度的速度向中点C运动,过点P作PQ⊥AB,交折线AD﹣DC于点Q,将线段PQ绕点P顺时针旋转90°,得到线段PR,连接QR.设△PQR与ABCD重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).
(1)当点R与点B重合时,求t的值;
(2)当点P在BC边上运动时,求线段PQ的长(用含有t的代数式表示);
(3)当点R落在ABCD的外部时,求S与t的函数关系式;
(4)直接写出点P运动过程中,△PCD是等腰三角形时所有的t值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,P,B,C是半径为8的⊙O上的四点,且满足∠BAC=∠APC=60°,

(1)求证:△ABC是等边三角形;
(2)求圆心O到BC的距离OD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,DE分别是边AB、AC上的点,且AD=CE,则∠ADC+∠BEA=( )
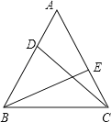
A.180°B.170°C.160°D.150°
查看答案和解析>>
科目:初中数学 来源: 题型:
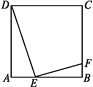
【题目】如图,E是正方形ABCD的边AB上的动点,EF⊥DE交BC于点F.
(1)求证:△ADE∽△BEF.
(2)设正方形的边长为4,AE=x,BF=y.当x取什么值时,y有最大值?并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一家糖果加工厂,它们要对一款奶糖进行包装,要求每袋净含量为100g.现使用甲、乙两种包装机同时包装100g的糖果,从中各抽出10袋,测得实际质量(g)如下:
甲:101,102,99,100,98,103,100,98,100,99
乙:100,101,100,98,101,97,100,98,103,102
(1)分别计算两组数据的平均数、众数、中位数;
(2)要想包装机包装奶糖质量比较稳定,你认为选择哪种包装机比较适合?简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() 于E,
于E,![]() ,D是AE上的一点,且
,D是AE上的一点,且![]() ,连接BD,CD.
,连接BD,CD.

![]() 试判断BD与AC的位置关系和数量关系,并说明理由;
试判断BD与AC的位置关系和数量关系,并说明理由;
![]() 如图2,若将
如图2,若将![]() 绕点E旋转一定的角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由;
绕点E旋转一定的角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由;
![]() 如图3,若将
如图3,若将![]() 中的等腰直角三角形都换成等边三角形,其他条件不变.
中的等腰直角三角形都换成等边三角形,其他条件不变.
![]() 试猜想BD与AC的数量关系,请直接写出结论;
试猜想BD与AC的数量关系,请直接写出结论;
![]() 你能求出BD与AC的夹角度数吗?如果能,请直接写出夹角度数;如果不能,请说明理由.
你能求出BD与AC的夹角度数吗?如果能,请直接写出夹角度数;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,点F是AC上的动点,BD=DF
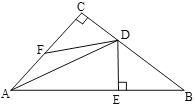
(1)求证:BE=FC;
(2)若∠B=30°,DC=2,此时![]() ,求△ACB的面积.
,求△ACB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com