
【题目】如果一个多位自然数的任意两个相邻数位上,左边数位上的数总比右边数位上数大1,那么我们把这样的自然数叫做“妙数”.例如:321,6543,98,…都是“妙数”.
(1)若某个“妙数”恰好等于其个位数的153倍,则这个“妙数”为 .
(2)证明:任意一个四位“妙数”减去任意一个两位“妙数”之差再加上1得到的结果一定能被11整除.
(3)在某个三位“妙数”的左侧放置一个一位自然数m作为千位上的数字,从而得到一新的四位自然数A,且m大于自然数A百位上的数字,否存在一个一位自然数n,使得自然数(9A+n)各数位上的数字全都相同?若存在请求出m和n的值;若不存在,请说明理由.
【答案】(1)765(2)证明见解析(3)m=9,n=4
【解析】
试题分析:(1)设这个“妙数”个位数字为a,根据题意判断“妙数”的尾位数,从而得知这个“妙数”为3位数,列出方程100(x+2)+10(x+1)+x=153x,求解可得;
(2)设四位“妙数”的个位为x、两位“妙数”的个位为y,分别表示出四位“妙数”和两位“妙数”,再将四位“妙数”减去任意一个两位“妙数”之差再加上1的结果除以11判断结果是否为整数即可;
(3)设三位“妙数”的个位为z,可知A=1000m+111z+210,继而可得9A+n=9000m+999z+1890+n=1000(9m+z+1)+800+90+n﹣z,由﹣8≤n﹣z≤9、1000(9m+z+1)≤1000(9×9+9+1)=91000知其百位数一定是8,且该数为5位数,若存在则该数为88888,从而得出![]() ,即9m+z=87、n﹣z=﹣2,由m>z+2知z<m﹣2,而z=87﹣9m<m﹣2,解之可得m>8.9,即可得m值,进一步即可得答案.
,即9m+z=87、n﹣z=﹣2,由m>z+2知z<m﹣2,而z=87﹣9m<m﹣2,解之可得m>8.9,即可得m值,进一步即可得答案.
试题解析:(1)设这个“妙数”个位数字为a,
若这个“妙数”为4位数,则其个位数字最大为6,根据题意可知这个“妙数”最大为6×153=918,不合题意;
∴这个“妙数”为3位数,根据题意得:100(x+2)+10(x+1)+x=153x,
解得:x=5,
则这个“妙数”为765,
故答案为:765;
(2)由题意,设四位“妙数”的个位为x,则此数为1000(x+3)+100(x+2)+10(x+1)+x=1111x+3210,
设两位“妙数”的个位为y,则此数为10(y+1)+y=11y+10,
∴![]() =101x﹣y+291,
=101x﹣y+291,
∵x、y为整数,
∴101x﹣y+291也为整数,
∴任意一个四位“妙数”减去任意一个两位“妙数”之差再加上1得到的结果一定能被11整除;
(3)设三位“妙数”的个位为z,由题意,得:
A=1000m+100(z+2)+10(z+1)+z=1000m+111z+210,
∴9A+n=9000m+999z+1890+n
=9000m+1000z+1890+n﹣z
=1000(9m+z+1)+800+90+n﹣z,
∵m、n是一位自然数,0≤z≤9,且z为整数,
∴﹣8≤n﹣z≤9,
∵9A+n的百位为8,且1000(9m+z+1)≤1000(9×9+9+1)=91000,
∴9A+n为五位数,且9A+n=88888,
∴![]() ,
,
∴9m+z=87,n﹣z=﹣2,
∵m>z+2,
∴z<m﹣2,
∴z=87﹣9m<m﹣2,
∴m>8.9,
∵m是一个自然数,
∴m=9,
于是z=6,n=4,
答:m=9,n=4.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】《杨辉算法》中有这么一道题:“直田积八百六十四步,只云长阔共六十步,问长多几何?”意思是:一块矩形田地的面积为864平方步,只知道它的长与宽共60步,问它的长比宽多了多少步?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,AD⊥BC于点D,点E为AC中点且BE平分∠ABD,连接BE交AD于点F,且BF=AC,过点D作DG∥AB,交AC于点G.
求证:
(1)∠BAD=2∠DAC
(2)EF=EG.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有4个黑球、2个白球,每个球除颜色外都相同,从中任意摸出3个球,下列事件为必然事件的是( )
A.至少有1个球是黑球
B.至少有1个球是白球
C.至少有2个球是黑球
D.至少有2个球是白球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生会准备调查七年级叙述参加“绘画类”、“书法类”、“乐器类”四类校本课程的人数,在全校进行随机抽样调查,并根据收集的数据绘制了如图两幅统计图(信息尚不完整),请根据图中提供的信息,解答下面的问题: 
(1)此次共调查了多少名同学?
(2)将条形图补充完整,并计算扇形统计图中乐器部分的圆心角的度数;
(3)如果该校共有1000名学生参加这4个课外兴趣小组,而每个教师最多只能辅导本组的25名学生,估计书法兴趣小组至少需要准备多少名教师?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生会准备调查七年级叙述参加“绘画类”、“书法类”、“乐器类”四类校本课程的人数,在全校进行随机抽样调查,并根据收集的数据绘制了如图两幅统计图(信息尚不完整),请根据图中提供的信息,解答下面的问题: 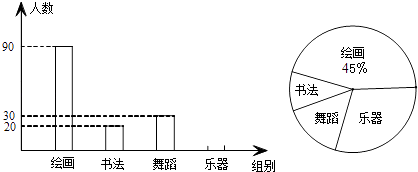
(1)此次共调查了多少名同学?
(2)将条形图补充完整,并计算扇形统计图中乐器部分的圆心角的度数;
(3)如果该校共有1000名学生参加这4个课外兴趣小组,而每个教师最多只能辅导本组的25名学生,估计书法兴趣小组至少需要准备多少名教师?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com