
【题目】《杨辉算法》中有这么一道题:“直田积八百六十四步,只云长阔共六十步,问长多几何?”意思是:一块矩形田地的面积为864平方步,只知道它的长与宽共60步,问它的长比宽多了多少步?
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC的延长线于点M,若∠A=40°.
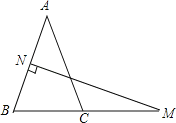
(1)求∠NMB的度数;
(2)如果将(1)中∠A的度数改为70°,其余条件不变,再求∠NMB的度数;
(3)你发现∠A与∠NMB有什么关系,试证明之.
查看答案和解析>>
科目:初中数学 来源: 题型:
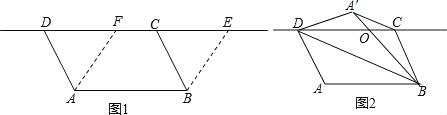
【题目】如图1,在ABEF中,AB=2,AF<AB,现将线段EF在直线EF上移动,在移动过程中,设线段EF的对应线段为CD,连接AD、BC.
(1)在上述移动过程中,对于四边形的说法不正确的是 B
A.面积保持不变 B.只有一个时刻为菱形
C.只有一个时刻为矩形 D.周长改变
(2)在上述移动过程中,如图2,若将△ABD沿着BD折叠得到△A′BD(点A′与点C不重合),A′B交CD于点O.
①试问A′C与BD平行吗?请说明理由;
②若以A′、D、B、C为顶点的四边形是矩形,且对角线的夹角为60°,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器超市销售每台进价分别为200元,170元的A、B两种型号的电风扇,表中是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
(进价、售价均保持不变,利润=销售收入﹣进货成本)
求A、B两种型号的电风扇的销售单价.
查看答案和解析>>
科目:初中数学 来源: 题型:
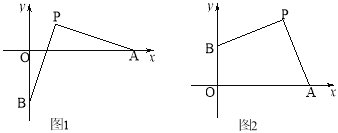
【题目】如图1,P(2,2),点A在x轴正半轴上运动,点B在y轴上运动,且PA=PB.
(1)求证:PA⊥PB;
(2)若点A(8,0),求点B的坐标;
(3)求OA – OB的值;
(4)如图2,若点B在y轴正半轴上运动时,直接写出OA+OB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个多位自然数的任意两个相邻数位上,左边数位上的数总比右边数位上数大1,那么我们把这样的自然数叫做“妙数”.例如:321,6543,98,…都是“妙数”.
(1)若某个“妙数”恰好等于其个位数的153倍,则这个“妙数”为 .
(2)证明:任意一个四位“妙数”减去任意一个两位“妙数”之差再加上1得到的结果一定能被11整除.
(3)在某个三位“妙数”的左侧放置一个一位自然数m作为千位上的数字,从而得到一新的四位自然数A,且m大于自然数A百位上的数字,否存在一个一位自然数n,使得自然数(9A+n)各数位上的数字全都相同?若存在请求出m和n的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com