Question

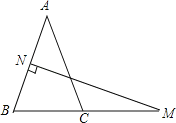
【题目】如图，在△ABC中，AB=AC，AB的垂直平分线交AB于点N，交BC的延长线于点M，若∠A=40°．

（1）求∠NMB的度数；

（2）如果将（1）中∠A的度数改为70°，其余条件不变，再求∠NMB的度数；

（3）你发现∠A与∠NMB有什么关系，试证明之．

Answer 1

【答案】（1）∠NMB=20°；（2）∠NMB =35°；（3）∠NMB=∠A，证明见解析.

【解析】试题分析：（1）由在△ABC中，AB=AC，∠A=40°，根据等腰三角形的性质，可求得∠ABC的度数，又由AB的垂直平分线交AB于点N，交BC的延长线于点M，即可求得答案；

（2）由在△ABC中，AB=AC，∠A=70°，根据等腰三角形的性质，可求得∠ABC的度数，又由AB的垂直平分线交AB于点N，交BC的延长线于点M，即可求得答案；

（3）由在△ABC中，AB=AC，根据等腰三角形的性质，即可用∠A表示出∠ABC，又由AB的垂直平分线交AB于点N，交BC的延长线于点M，即可求得答案．

试题解析：（1）∵在△ABC中，AB=AC，∠A=40°，

∴∠ABC=∠ACB=70°，

∵AB的垂直平分线交AB于点N，交BC的延长线于点M，

∴MN⊥AB，

∴∠NMB=90°∠ABC=20°；

（2）∵在△ABC中，AB=AC，∠A=70°，

∴∠ABC=∠ACB=55°，

∵AB的垂直平分线交AB于点N，交BC的延长线于点M，

∴MN⊥AB，

∴∠NMB=90°∠ABC=35°；

（3）∠NMB=∠A.

理由：∵在△ABC中，AB=AC，

∴∠ABC=∠ACB=，

∵AB的垂直平分线交AB于点N，交BC的延长线于点M，

∴MN⊥AB，

∴∠NMB=90°∠ABC=∠A.