Question

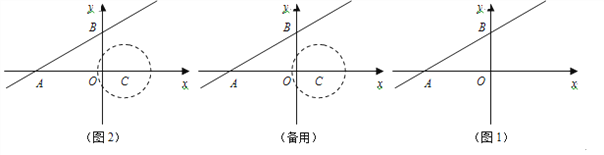
【题目】如图1，在平面直角坐标系中，过点（， ）的直线交轴的正半轴于点， ．

（1）求直线的解析式；（直接写出结果）

（2）如图2，点是轴上一动点，以为圆心， 为半径作⊙，当⊙与相切时，设切点为，求圆心的坐标；

（3）在（2）的条件下，点在轴上，△是以为底边的等腰三角形，求过点、、三点的抛物线．

Answer 1

【答案】（1）直线的解析式为；

（2）当⊙与相切时，点坐标为（， ）或（， ）；

（3）过点、、三点的抛物线为或

【解析】试题分析：(1)、根据Rt△AOB的性质求出点B的坐标，然后根据待定系数法求出函数解析式；(2)、根据⊙在直线AB的左侧和右侧两种情况以及圆的切线的性质分别求出AC的长度，从而得出点C的坐标；(3)、本题也需要分两种情况进行讨论：⊙在直线的右侧相切时得出点D的坐标，根据等边△的性质得出的坐标，从而根据待定系数法求出抛物线的解析式；⊙在直线的左侧相切时，根据切线的直角三角形的性质求出点的坐标，根据待定系数法求出抛物线的解析式.

试题解析：（1）∵（， ），∴． 在Rt△中， ．

， ． ． ∴（， ）．

设直线的解析式为．

则 解得 ∴直线的解析式为．

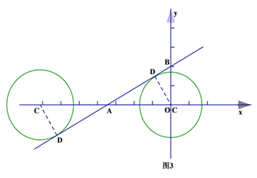
（2）如图3，①当⊙在直线的左侧时， ∵⊙与相切，∴．

在Rt△中， ． ， ， ．

而，∴与重合，即坐标为（， ）．

②根据对称性，⊙还可能在直线的右侧，与直线相切，此时．

∴坐标为（， ）．

综上，当⊙与相切时，点坐标为（， ）或（， ）．

（3）如图4，①⊙ 在直线的右侧相切时，点的坐标为（， ）．

此时△为等边三角形．∴（， ）．

设过点、、三点的抛物线的解析式为．

则 ∴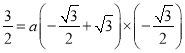

②当⊙在直线的左侧相切时， （， ）

设，则， ． 在Rt△中， ．

， 即，

∴（， ）．

设过点、、三点的抛物线的解析式为．

则， ． ．

综上，过点、、三点的抛物线为或．