
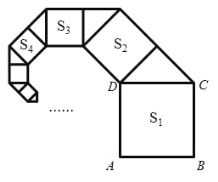
【题目】如图,正方形 ABCD 的边长为1,其面积为 S1,以CD 为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积记为 S2,…,按此规律继续下去,则 S9的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2﹣4x+c的图象经过坐标原点,与x轴交于点A(﹣4,0).

(1)求二次函数的解析式;
(2)在抛物线上存在点P,满足S△AOP=8,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数y1=x+5的图象与x轴交于点A,一次函数y2=-2x+b的图象分别与x轴、y轴交于点B,C,且与y1=x+5的图象交于点D(m,4).

(1)求m,b的值;
(2)若y1>y2,则x的取值范围是 ;
(3)求四边形AOCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
我们知道方程2x+3y=12有无数组解,但在实际生活中我们往往只需要求出其正整数解.例:由2x+3y=12,得y=![]() =4-
=4-![]() x,(x、y为正整数)
x,(x、y为正整数)
∴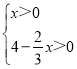 则有0<x<6
则有0<x<6
又y=4-![]() x为正整数,则
x为正整数,则![]() x为正整数.
x为正整数.
从而x=3,代入y=4-![]() ×3=2
×3=2
∴2x+3y=12的正整数解为![]() .
.
利用以上方法解决下列问题:
七年级某班为了奖励学习进步的学生,购买了单价为3元的笔记本与单价为5元的钢笔两种奖品,共花费35元,问有几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
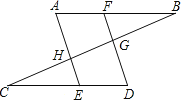
【题目】已知,如图,点F在AB上,点E在CD上,AE、DF分别交BC与H,G,∠A=∠D,∠FGB+∠EHG=180°.
(1)求证:AB∥CD;
(2)若AE⊥BC,直接写出图中所有与∠C互余的角,不需要证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E,D是抛物线的顶点.
(1)求此抛物线的解析式;
(2)直接写出点C和点D的坐标;
(3)若点P在第一象限内的抛物线上,且S△ABP=4S△COE,求P点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式y=a(x﹣4)2+h,已知点O与球网的水平距离为5m,球网的高度为1.55m.

(1)当a=﹣![]() 时,①求h的值;②通过计算判断此球能否过网.
时,①求h的值;②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为![]() m的Q处时,乙扣球成功,求a的值.
m的Q处时,乙扣球成功,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线ll,l2交于点O,点P关于ll,l2的对称点分别为P1、P2.
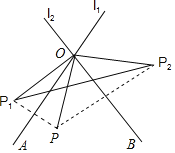
(1)若ll,l2相交所成的锐角∠AOB=60°,则∠P1OP2=______;
(2)若OP=3,P1P2=5,求△P1OP2的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com