
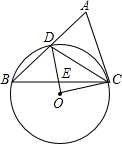
 如图,在△ABC中,D是AB边上一点,⊙O过D、B、C三点,∠DOC=2∠ACD=90°.
如图,在△ABC中,D是AB边上一点,⊙O过D、B、C三点,∠DOC=2∠ACD=90°.分析 (1)由∠DOC=2∠ACD=90°易得∠ACD=45°,△OCD为等腰直角三角形,则∠OCD=45°,于是可计算出∠OCA=90°,则可根据切线的判定定理得到直线AC是⊙O的切线;
(2)①由于∠ACB=75°,∠ACD=45°则∠DCB=30°,由△OCD为等腰直角三角形得到CD=$\sqrt{2}$OC=2$\sqrt{2}$,根据圆周角定理得到∠DBC=$\frac{1}{2}$∠COD=45°,作DH⊥BC于H,如图,利用解直角三角形,先在Rt△CDH中求出DH=$\frac{1}{2}$CD=$\sqrt{2}$,然后在Rt△BDH中可计算出BD的长;
②设⊙O的半径r,则CD=$\sqrt{2}$r,与①一样先求出DH=$\frac{1}{2}$CD=$\frac{\sqrt{2}}{2}$r,CH=$\sqrt{3}$DH=$\frac{\sqrt{6}}{2}$r,再求出BH=DH=$\frac{\sqrt{2}}{2}$r,所以BC=BH+CH=$\frac{\sqrt{6}+\sqrt{2}}{2}$r,然后$\frac{CD}{BC}$的值.
解答 (1)证明:∵∠DOC=2∠ACD=90°,
∴∠ACD=45°,△OCD为等腰直角三角形,
∴∠OCD=45°,
∴∠OCA=∠OCD+∠ACD=90°,
∴OC⊥AC,
∴直线AC是⊙O的切线;
(2)解:①∵∠ACB=75°,∠ACD=45°,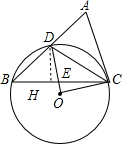
∴∠DCB=30°,
∵△OCD为等腰直角三角形,
∴CD=$\sqrt{2}$OC=2$\sqrt{2}$,∠DBC=$\frac{1}{2}$∠COD=45°,
作DH⊥BC于H,如图,
在Rt△CDH中,∵∠DCH=30°,
∴DH=$\frac{1}{2}$CD=$\frac{1}{2}$×2$\sqrt{2}$=$\sqrt{2}$,
在Rt△BDH中,∵∠DBH=45°,
∴BD=$\sqrt{2}$DH=$\sqrt{2}$×$\sqrt{2}$=2;
②CD:BC的值是定值.
设⊙O的半径r,则CD=$\sqrt{2}$r,
在Rt△CDH中,∵∠DCH=30°,
∴DH=$\frac{1}{2}$CD=$\frac{\sqrt{2}}{2}$r,
CH=$\sqrt{3}$DH=$\frac{\sqrt{6}}{2}$r,
在Rt△BDH中,∵∠DBH=45°,
∴BH=DH=$\frac{\sqrt{2}}{2}$r,
∴BC=BH+CH=$\frac{\sqrt{6}+\sqrt{2}}{2}$r,
∴$\frac{CD}{BC}$=$\frac{\sqrt{2}r}{\frac{\sqrt{6}+\sqrt{2}}{2}r}$=$\frac{2}{\sqrt{3}+1}$=$\sqrt{3}$-1.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了解直角三角形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
| 月均用水量x/m3 | 0<x≤5 | 5<x≤10 | 10<x≤15 | 15<x≤20 | x>20 |
| 频数/户 | 12 | 20 | 3 | ||
| 频率 | 0.12 | 0.07 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2014 | B. | 2014.5 | C. | 2015 | D. | 2015.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,管中放置着三根同样的绳子AA1、BB1、CC1,小明先从左端A、B、C三个绳头中随机选两个打一个结,再从右端A1、B1、C1三个绳头中随机选两个打一个结,请用树状图或列表法求着三根绳子能连结成一根长绳的概率.
如图,管中放置着三根同样的绳子AA1、BB1、CC1,小明先从左端A、B、C三个绳头中随机选两个打一个结,再从右端A1、B1、C1三个绳头中随机选两个打一个结,请用树状图或列表法求着三根绳子能连结成一根长绳的概率.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=3x+2 | B. | y=3x-2 | C. | y=3x+6 | D. | y=3x-6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
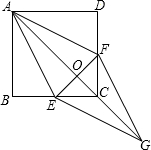 如图,正方形ABCD中,点E、F分别在边BC、CD上,AE=AF,AC和EF交于点O,延长AC至点G,使得AO=OG,连接EG、FG.
如图,正方形ABCD中,点E、F分别在边BC、CD上,AE=AF,AC和EF交于点O,延长AC至点G,使得AO=OG,连接EG、FG.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com