
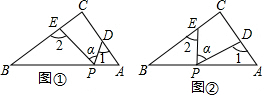
分析 (1)连接PC,根据三角形的一个外角等于与它不相邻的两个内角的和可得∠1=∠PCD+∠CPD,∠2=∠PCE+∠CPE,再表示出∠1+∠2即可;
(2)利用(1)中所求得出答案即可.
解答 解:(1)如图,连接PC,
∵∠1=∠PCD+∠CPD,∠2=∠PCE+∠CPE,
∴∠1+∠2=∠PCD+∠CPD+∠PCE+∠CPE=∠DPE+∠C,
∵∠DPE=∠α=65°,∠C=90°,
∴∠1+∠2=65°+90°=155°,
故答案为:155°;
(2)连接PC,
∵∠1=∠PCD+∠CPD,∠2=∠PCE+∠CPE,
∴∠1+∠2=∠PCD+∠CPD+∠PCE+∠CPE=∠DPE+∠C,
∵∠C=90°,∠DPE=∠α,
∴∠1+∠2=90°+∠α;
点评 本题考查了三角形内角和定理和外角的性质、对顶角相等的性质,熟练利用三角形外角的性质是解题的关键.


 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若两角之和为90°,则这两个角互余 | B. | 延长线段AO到点C,使OC=OA | ||
| C. | 平角是一条直线 | D. | 相等的角是对顶角 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | |-2|与2 | B. | -2与-$\frac{1}{2}$ | C. | -2与$\root{3}{-8}$ | D. | -3与$\sqrt{(-3)^{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
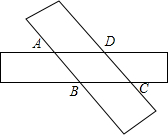 如图,两张宽为1cm的矩形纸条交叉叠放,其中重叠部分部分是四边形ABCD,
如图,两张宽为1cm的矩形纸条交叉叠放,其中重叠部分部分是四边形ABCD,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com