
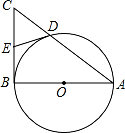
| 解:(1)DE与半圆O相切. 证明:连接OD、OE. ∵O、E分别是BA、BC的中点, ∴OE∥AC, ∴∠BOE=∠BAC,∠EOD=∠ADO, ∵OA=OD, ∴∠ADO=∠BAC. ∴∠BOE=∠EOD. ∵OD=OB,OE=OE, ∴△OBE≌△ODE. ∴∠ODE=∠OBE=90°. ∴DE与半圆O相切; (2)∵在Rt△ABC中,BD⊥AC, ∴Rt△ABD∽Rt△ABC, ∴ 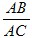 = =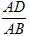 ,即AB2=AD·AC, ,即AB2=AD·AC,∴AC= 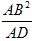 . .∵AD,AB的长是方程x2﹣10x+24=0的两个根, ∴解方程x2﹣10x+24=0,得:x1=4,x2=6. ∵AD<AB, ∴AD=4,AB=6, ∵AC= 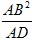 ,AD=4,AB=6, ,AD=4,AB=6,∴AC=9, 在Rt△ABC中,AB=6,AC=9. ∴BC=  = =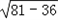 =3 =3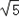 . . |
 |


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
| 4 |
| 3 |
| 4 |
| 3 |

查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
| ||
| 8 |

查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•咸丰县二模)如图,已知在Rt△ABC中,∠ACB=90°,AB=10,分别以AC、BC为直经作半圆,面积分别记为S1、S2,则S1+S2的值等于( )
(2012•咸丰县二模)如图,已知在Rt△ABC中,∠ACB=90°,AB=10,分别以AC、BC为直经作半圆,面积分别记为S1、S2,则S1+S2的值等于( )查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
| 2 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com