Question

8．我们知道，在同一平面内两条直线相交只有一个交点，三条直线两两相交最少一个交点．
（1）同一平面内的四条直线，最少有几个交点？最多有几个交点？
（2）同一平面内的五条直线，最多有几个交点？
（3）请探究；同一平面内若有n条直线两两相交，则最多有几个交点？（用含n的代表式表示）．

Answer 1

分析 （1）、（2）可通过画图得出交点个数．
（3）通过以上两题找出规律解答．

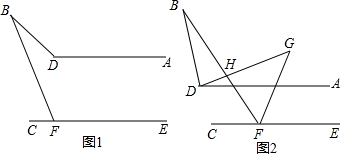
解答 解：（1）如图1，同一平面内的四条直线两两相交，最少有1个交点，最多有6个交点，

可得四条直线两两相交，最多有3个交点；
（2）如图2，同一平面内的五条直线，最多有10个交点，
；

可得4条直线两两相交，最多有6个交点；
（3）由（1）得，$\frac{4×（4-1）}{2}$=6，
由（2）得，$\frac{5×（5-1）}{2}$=10，
∴可得，n条直线两两相交，最多有$\frac{n（n-1）}{2}$个交点（n为正整数，且n≥2）．

点评 本题考查了图形的变化，是一道关于数字猜想的问题，关键是通过归纳与总结，得到其中的规律．