Question

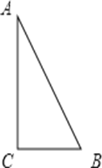
【题目】如图,△ABC中,∠C=90°,AB=5cm，BC=3cm,,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.

(1)出发2秒后,求△ABP的周长.

(2)问t为何值时,△BCP为等腰三角形?

(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?

Answer 1

【答案】(1) 7+;(2) t为3s、5.4s、6s、6.5s;(3) t为2或6秒.

【解析】

（1）根据速度为每秒1cm，求出出发2秒后CP的长，然后就知AP的长，利用勾股定理求得PB的长，最后即可求得周长．
（2）因为AB与CB，由勾股定理得AC=4 因为AB为5cm，所以必须使AC=CB，或CB=AB，所以必须使AC或AB等于3，有两种情况，△BCP为等腰三角形．
（3）分类讨论：当P点在AC上，Q在AB上，则PC=t，BQ=2t-3，t+2t-3=6；当P点在AB上，Q在AC上，则AC=t-4，AQ=2t-8，t-4+2t-8=6．

解：（1）如图1，由∠C=90°，AB=5cm，BC=3cm，
∴AC=4，动点P从点C开始，按C→A→B→C的路径运动，且速度为每秒1cm，
∴出发2秒后，则CP=2，
∵∠C=90°，
∴PB==，
∴△ABP的周长为：AP+PB+AB=2+5+=7+．

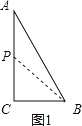
（2）①如图2，若P在边AC上时，BC=CP=3cm，
此时用的时间为3s，△BCP为等腰三角形；

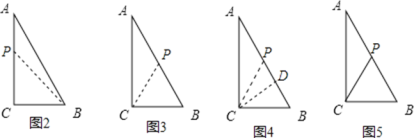
②若P在AB边上时，有三种情况：
i）如图3，若使BP=CB=3cm，此时AP=2cm，P运动的路程为2+4=6cm，
所以用的时间为6s，△BCP为等腰三角形；
ii）如图4，若CP=BC=3cm，过C作斜边AB的高，根据面积法求得高为2.4cm，
作CD⊥AB于点D，
在Rt△PCD中，PD==1.8，
所以BP=2PD=3.6cm，
所以P运动的路程为9-3.6=5.4cm，
则用的时间为5.4s，△BCP为等腰三角形；
ⅲ）如图5，若BP=CP，此时P应该为斜边AB的中点，P运动的路程为4+2.5=6.5cm
则所用的时间为6.5s，△BCP为等腰三角形；
综上所述，当t为3s、5.4s、6s、6.5s时，△BCP为等腰三角形
（3）如图6，当P点在AC上，Q在AB上，则PC=t，BQ=2t-3，
∵直线PQ把△ABC的周长分成相等的两部分，
∴t+2t-3=3，
∴t=2；

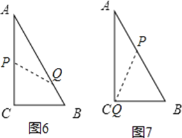
如图7，当P点在AB上，Q在AC上，则AP=t-4，AQ=2t-8，
∵直线PQ把△ABC的周长分成相等的两部分，
∴t-4+2t-8=6，
∴t=6，
∴当t为2或6秒时，直线PQ把△ABC的周长分成相等的两部分．