
【题目】(1)先观察下列等式,再完成题后问题:
![]() ,
,![]() ,
,![]()
①请你猜想:![]() =________.
=________.
②若a、b为有理数,且![]() ,
,
求:![]() +…+
+…+![]() 的值.
的值.
(2)探究并计算:![]() +
+![]() +
+![]() +…+
+…+![]()
(3)如图,把一个面积为1的正方形等分成两个面积为![]() 的长方形,接着把面积为
的长方形,接着把面积为![]() 的长方形等分成两个面积为
的长方形等分成两个面积为![]() 的正方形,再把面积为
的正方形,再把面积为![]() 的正方形等分成两个面积为
的正方形等分成两个面积为![]() 的矩形.如此进行下去,试利用图形揭示的规律计算:
的矩形.如此进行下去,试利用图形揭示的规律计算:![]() +
+![]() +
+![]() +
+![]() +
+![]() +
+![]() +
+![]() .(直接写答案).
.(直接写答案).

科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC长为( )

A. 10 B. 8 C. 14 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)【证法回顾】证明:三角形中位线定理.
已知:如图1,DE是△ABC的中位线.
求证: .
证明:添加辅助线:如图1,在△ABC中,延长DE (D、E分别是AB、AC的中点)到点F,使得EF=DE,连接CF;
请继续完成证明过程:

(2)【问题解决】
如图2,在正方形ABCD中,E为AD的中点,G、F分别为AB、CD边上的点,若AG=2,DF=3,∠GEF=90°,求GF的长.
(3)【拓展研究】
如图3,在四边形ABCD中,∠A=105°,∠D=120°,E为AD的中点,G、F分别为AB、CD边上的点,若AG=![]() ,DF=2,∠GEF=90°,求GF的长.
,DF=2,∠GEF=90°,求GF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家经销一种绿茶,用于装修门面已投资3000元,已知绿茶每千克成本50元,在第一个月的试销时间内发现,销量w(kg)随销售单价x(元/kg)的变化而变化,具体变化规律如下表所示
销售单价x(元/kg) | … | 70 | 75 | 80 | 85 | 90 | … |
销售量w(kg) | … | 100 | 90 | 80 | 70 | 60 | … |
设该绿茶的月销售利润为y(元)(销售利润=单价×销售量﹣成本﹣投资).
(1)请根据上表,写出w与x之间的函数关系式(不必写出自变量x的取值范围);
(2)求y与x之间的函数关系式(不必写出自变量x的取值范围).并求出x为何值时,y的值最大?
(3)若在第一个月里,按使y获得最大值的销售单价进行销售后,在第二个月里受物价部门干预,销售单价不得高于90元,要想在全部收回投资的基础上使第二个月的利润达到1700元,那么第二个月里应该确定销售单价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一次数学活动课上,小颖用 10 个棱长为 1 的正方体积木搭成一个几何体,然后她请小华用其 他棱长为 1 的正方体积木在旁边再搭一个几何体,使用小华所搭几何体恰好和小颖所搭几何体拼成一个 无空隙的大正方体(不改变小颖所搭几何体的形状).那么:按照小颖的要求搭几何体,小华至少需要_____个正方体积木.按照小颖的要求,小华所搭几何体的表面积最小为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,铁路上A,B两点相距25 km,C,D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=16 km,CB=11 km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?

查看答案和解析>>
科目:初中数学 来源: 题型:
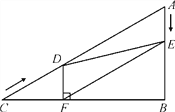
【题目】如图,在Rt△ABC中,∠B=90°,AC=60 cm,∠A=60°,点D从点C出发沿CA方向以4 cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2 cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF。
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角尺如图拼接:含![]() 角的三角尺
角的三角尺![]() 的长直角边与含
的长直角边与含![]() 角的三角尺
角的三角尺![]() 的斜边恰好重合
的斜边恰好重合![]() 已知
已知![]() 是AC上的一个动点.
是AC上的一个动点.
![]() 当点P运动到
当点P运动到![]() 的平分线上时,连接DP,求DP的长;
的平分线上时,连接DP,求DP的长;
![]() 当点P在运动过程中出现
当点P在运动过程中出现![]() 时,求此时
时,求此时![]() 的度数;
的度数;
![]() 当点P运动到什么位置时,以
当点P运动到什么位置时,以![]() 为顶点的平行四边形的顶点Q恰好在边BC上?求出此时DPBQ的面积.
为顶点的平行四边形的顶点Q恰好在边BC上?求出此时DPBQ的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com