
 如图,点D是线段BC的中点,分别以点B,C为圆心,BC长为半径画弧,两弧相交于点A,连接AB,AC,AD,点E为AD上一点,连接BE,CE.
如图,点D是线段BC的中点,分别以点B,C为圆心,BC长为半径画弧,两弧相交于点A,连接AB,AC,AD,点E为AD上一点,连接BE,CE.
(1)求证:BE =CE;
=CE;
(2)以点E为圆心,ED长为半径画弧,分别交BE,CE于点F, G.若BC=4,∠EBD=30°,求图中阴影部分(扇形)的面积.
G.若BC=4,∠EBD=30°,求图中阴影部分(扇形)的面积.

(1)证明:∵点D是线段BC的中点,
∴BD=CD,
∵AB=AC=BC,
∴△ABC为等边三角形,
∴AD为BC的垂直平分线,
∴BE=CE;
(2)解:∵EB=EC,
∴∠EBC =∠ECB=30°,
=∠ECB=30°,
∴∠BEC=120°,
在Rt△BDE中,BD=BC=2,∠EBD=30°,
∴ED=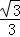 BD=
BD=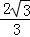 ,
,
∴阴影部分(扇形)的面积=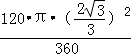 =π.10.解:如图3-172所示,作DH⊥BC于点H,∴DH=AB=2,CH=BC-BH=BC-AD=7-3=4.在Rt△CDH中,CD=
=π.10.解:如图3-172所示,作DH⊥BC于点H,∴DH=AB=2,CH=BC-BH=BC-AD=7-3=4.在Rt△CDH中,CD=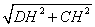 =
=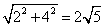 .∴S表=S圆锥侧+S圆柱侧+S底=π·DH·CD+2π·AB·AD+π·(AB)2=π×2×
.∴S表=S圆锥侧+S圆柱侧+S底=π·DH·CD+2π·AB·AD+π·(AB)2=π×2×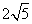 +2π×2×3+π×22=
+2π×2×3+π×22=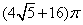 .
.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
如图1,PA、PB分别切圆O于A、B两点,C为劣弧AB上一点,∠APB=30°,则∠ACB=( ).
A.60° B.75° C.105° D.120°
C.105° D.120°

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在4×4的正方形网格中,每个小正方形的边长为1,若将△AOC绕点O顺时针旋转90°得到△BOD,则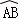 的长为( )
的长为( )
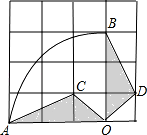
A π B 6π C 3π D 1.5π
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在正方形ABCD中,对角线BD的长为 .若将BD绕点B旋转后,点D落在BC延长线上的点D′处,点D经过的路径为
.若将BD绕点B旋转后,点D落在BC延长线上的点D′处,点D经过的路径为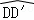 ,则图中阴影部分的面积是( )
,则图中阴影部分的面积是( )
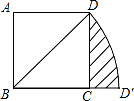
A 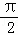 ﹣1 B
﹣1 B 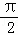 ﹣2 C
﹣2 C 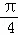 ﹣1 D π﹣2
﹣1 D π﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
如图3-150所示,AB是半圆O的直径,以O为圆心,OE为半径的半圆交AB于E,F两点,弦AC切小半圆于点D.已知AO=4,EO=2,那么阴影部分的面积是 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com