
分析 利用根与系数的关系表示出两根之和与两根之积,判断出两根之积小于0,得到两根异号,分两种情况考虑:若x1>0,x2<0,利用绝对值的代数意义化简已知的等式,将表示出的两根之和代入,列出关于m的方程,求出方程的解得到m的值;若x1<0,x2>0,同理求出m的值.
解答 解:∵关于x的一元二次方程x2-(m-3)x-m2=0的两个实数根为x1,x2,
∴x1•x2=-m2≤0,x1+x2=m-3,
∴x1,x2异号,
又|x1|=|x2|-2,即|x1|-|x2|=-2,
若x1>0,x2<0,上式化简得:x1+x2=-2,
∴m-3=-2,即m=1;
若x1<0,x2>0,上式化简得:-(x1+x2)=-2,
∴x1+x2=m-3=2,即m=5.
点评 此题考查了一元二次方程根与系数的关系:x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC为等腰三角形,AB=AC,D为△ABC内一点,连接AD,将线段AD绕点A旋转至AE,使得∠DAE=∠BAC,F,G,H分别为BC,CD,DE的中点,连接BD,CE,GF,GH.
如图,△ABC为等腰三角形,AB=AC,D为△ABC内一点,连接AD,将线段AD绕点A旋转至AE,使得∠DAE=∠BAC,F,G,H分别为BC,CD,DE的中点,连接BD,CE,GF,GH.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
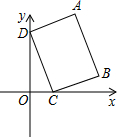 如图,在平面直角坐标系中,长方形ABCD的顶点C、D分别在x轴、y轴的正半轴上,顶点A、B在第一象限,其中顶点B的坐标是(3,1),顶点D的坐标是(0,3),线段AB=$\sqrt{10}$,则顶点A的坐标是( )
如图,在平面直角坐标系中,长方形ABCD的顶点C、D分别在x轴、y轴的正半轴上,顶点A、B在第一象限,其中顶点B的坐标是(3,1),顶点D的坐标是(0,3),线段AB=$\sqrt{10}$,则顶点A的坐标是( )| A. | (2,4) | B. | ($\frac{5}{2}$,4) | C. | (3,4) | D. | (2,5) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com