
【题目】已知m+n=7,点A(m,n)在一个反比例函数的图象上,点A与坐标原点的距离为5,现将这个反比例函数图象绕原点顺时针旋转90o,得到一个新的反比例函数图象,则这个新的反比例函数的解析式是________.
科目:初中数学 来源: 题型:
【题目】某水果店销售某品牌苹果,该苹果每箱的进价是40元,若每箱售价60元,每星期可卖180箱.为了促销,该水果店决定降价销售.市场调查反映:若售价每降价1元,每星期可多卖10箱.设该苹果每箱售价x元(40≤x≤60),每星期的销售量为y箱.
(1)求y与x之间的函数关系式;
(2)当每箱售价为多少元时,每星期的销售利润达到3570元?
(3)当每箱售价为多少元时,每星期的销售利润最大,最大利润多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元旦期间,某超市销售两种不同品牌的苹果,已知1千克甲种苹果和1千克乙种苹果的进价之和为18元.当销售1千克甲种苹果和1千克乙种苹果利润分别为4元和2元时,陈老师购买3千克甲种苹果和4千克乙种苹果共用82元.
(1)求甲、乙两种苹果的进价分别是每千克多少元?
(2)在(1)的情况下,超市平均每天可售出甲种苹果100千克和乙种苹果140千克,若将这两种苹果的售价各提高1元,则超市每天这两种苹果均少售出10千克,超市决定把这两种苹果的售价提高x元,在不考虑其他因素的条件下,使超市销售这两种苹果共获利960元,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD,DE交BC于F,交AB的延长线于E,且∠EDB=∠C.
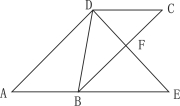
(1)求证:△ADE∽△DBE;
(2)若DE=9cm,AE=12cm,求DC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
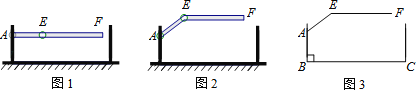
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
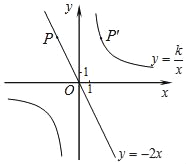
【题目】如图,已知直线y=﹣2x经过点P(﹣2,a),点P关于y轴的对称点P′在反比例函数y=![]() (k≠0)的图象上.
(k≠0)的图象上.
(1)求反比例函数的解析式;
(2)直接写出当y<4时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一条自南向北的大道上有O、A两个景点,O、A相距20km,在O处测得另一景点C位于点O的北偏东37°方向,在A处测得景点C位于点A的南偏东76°方向,且A、C相距13km .
(1)求:①A到OC之间的距离;
②O、C两景点之间的距离;
(2)若在O处测得景点B 位于景点O的正东方向10km,求B、C两景点之间的距离.(参考数据:tan37°=0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90,AC=BC=1,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M,垂足分别为H、G.现有以下结论:①AB=![]() ;②当点E与点B重合时,MH=
;②当点E与点B重合时,MH=![]() ;③AF+BE=EF;④MGMH=
;③AF+BE=EF;④MGMH=![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com