
【题目】如图,一条自南向北的大道上有O、A两个景点,O、A相距20km,在O处测得另一景点C位于点O的北偏东37°方向,在A处测得景点C位于点A的南偏东76°方向,且A、C相距13km .
(1)求:①A到OC之间的距离;
②O、C两景点之间的距离;
(2)若在O处测得景点B 位于景点O的正东方向10km,求B、C两景点之间的距离.(参考数据:tan37°=0.75)

【答案】(1)①16km②21km(2)17km
【解析】
(1)①作AH⊥OC于H,解直角三角形AHO即可得解;
②在Rt△AHC中,HC=5,故可求OC的长;
(2)作BG⊥OC于G,可求![]() ,再由勾股定理求出BC即可.
,再由勾股定理求出BC即可.
(1)①作AH⊥OC于H,
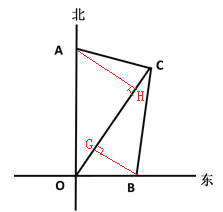
∵tan∠AOC=0.75,∴![]() ,
,
设AH=3x,则OH=4x,由勾股定理得,(3x)2+(4x)2=202,
解得,x=4,则AH=12,0H=16km
②在Rt△AHC中,HC=![]() =5,∴OC=OH+HC=21km
=5,∴OC=OH+HC=21km
(2) 作BG⊥OC于G,∵∠AOC+∠COB=90°,∠BOC+∠OBG=90°,
∴∠AOC=∠OBG,
∴![]() ,又OB=10, ∴OG=6,BG=8,
,又OB=10, ∴OG=6,BG=8,
∴CG=OC﹣OG=15,
∴BC=![]() =17km
=17km


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为6,E,F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.

(1)求证:EF=MF;
(2)若AE=2,求FC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知m+n=7,点A(m,n)在一个反比例函数的图象上,点A与坐标原点的距离为5,现将这个反比例函数图象绕原点顺时针旋转90o,得到一个新的反比例函数图象,则这个新的反比例函数的解析式是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A是反比例函数y=![]() (x>0)的图象上的一个动点,连接OA,OB⊥OA,且OB=2OA,那么经过点B的反比例函数图象的表达式为( )
(x>0)的图象上的一个动点,连接OA,OB⊥OA,且OB=2OA,那么经过点B的反比例函数图象的表达式为( )
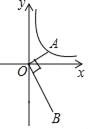
A. y=﹣![]() B. y=
B. y=![]() C. y=﹣
C. y=﹣![]() D. y=
D. y=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知二次函数![]() (a>0)图像与x轴交于点A、B(点A在点B的左侧),与y轴的交于点C,顶点为D .
(a>0)图像与x轴交于点A、B(点A在点B的左侧),与y轴的交于点C,顶点为D .
(1)求点A、B的坐标;
(2)若M为对称轴与x轴交点,且DM=2AM,
①求二次函数解析式;
②当30°<∠ADM<45°时,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
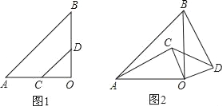
【题目】如图1、图2,△AOB,△COD均是等腰直角三角形,∠AOB=∠COD=90°,
(1)在图1中,AC与BD相等吗?请说明理由;
(2)若△COD绕点O顺时针旋转一定角度后,到达图2的位置,请问AC与BD还相等吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A、B两点的坐标分别为(―2,0),(0,1),⊙C的圆心坐标为(0,―1),半径为1.若D是⊙C上的一个动点,射线AD与y轴交于点E,则△ABE面积的最大值是( ) 
A. 4 B. ![]() C.
C. ![]() D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
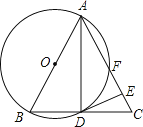
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O与BC交于点D,与AC交于点F,过点D作⊙O的切线交AC于E.
(1)求证:AD2=ABAE;
(2)若AD=2![]() ,AF=3,求⊙O的半径.
,AF=3,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com