
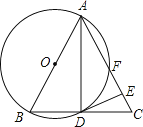
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O与BC交于点D,与AC交于点F,过点D作⊙O的切线交AC于E.
(1)求证:AD2=ABAE;
(2)若AD=2![]() ,AF=3,求⊙O的半径.
,AF=3,求⊙O的半径.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)欲证明AD2=ABAE,即证明AD2=ACAE,只要证明△ADE∽△ACD即可.
(2)易知OD=![]() AC,只要求出AC,先证明EF=EC,设EF=EC=x,根据DE2=EFEA=AD2-AE2,列出方程即可解决问题.
AC,只要求出AC,先证明EF=EC,设EF=EC=x,根据DE2=EFEA=AD2-AE2,列出方程即可解决问题.
(1)如图,连接OD,DF.
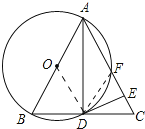
∵AB是直径,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴BD=DC,
∵AO=OB,
∴OD∥AC,DO=![]() AC,
AC,
∵DE是切线,
∴OD⊥DE,∵OD∥AC,
∴DE⊥AC,
∴∠AED=90°,
∵∠DAE=∠DAC,∠AED=∠ADC=90°,
∴△ADE∽△ACD,
∴![]() ,
,
∴AD2=AEAC=ABAE.
(2)∵AB=AC,
∴∠B=∠C,
∵∠DFC=∠B,
∴∠C=∠DFC,
∴DF=DC,∵DE⊥CF,
∴EF=EC,设FE=EC=x,
∵DE是切线
∴DE2=EFEA=AD2-AE2,
∴x(x+3)=(2![]() )2-(x+3)2,
)2-(x+3)2,
∴x=![]() ,
,
∴AC=AF+FC=3+![]() =
=![]() ,
,
由(1)可知OD=![]() AC=
AC=![]() ,
,
∴⊙O的半径为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,一条自南向北的大道上有O、A两个景点,O、A相距20km,在O处测得另一景点C位于点O的北偏东37°方向,在A处测得景点C位于点A的南偏东76°方向,且A、C相距13km .
(1)求:①A到OC之间的距离;
②O、C两景点之间的距离;
(2)若在O处测得景点B 位于景点O的正东方向10km,求B、C两景点之间的距离.(参考数据:tan37°=0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90,AC=BC=1,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M,垂足分别为H、G.现有以下结论:①AB=![]() ;②当点E与点B重合时,MH=
;②当点E与点B重合时,MH=![]() ;③AF+BE=EF;④MGMH=
;③AF+BE=EF;④MGMH=![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,商场服装部统计了每位营业员在某月的销售额(单位:万元),数据如下:
17 | 18 | 16 | 13 | 24 | 15 | 28 | 26 | 18 | 19 |
22 | 17 | 16 | 19 | 32 | 30 | 16 | 14 | 15 | 26 |
15 | 32 | 23 | 17 | 15 | 15 | 28 | 28 | 16 | 19 |
对这30个数据按组距3进行分组,并整理、描述和分析如下.
频数分布表
组别 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
销售额 |
|
|
|
|
|
|
|
频数 | 7 | 9 | 3 |
| 2 |
| 2 |
数据分析表
平均数 | 众数 | 中位数 |
20.3 |
| 18 |
请根据以上信息解答下列问题:
(1)填空:a= ,b= ,c= ;
(2)若将月销售额不低于25万元确定为销售目标,则有 位营业员获得奖励;
(3)若想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区举行“庆祝改革开放40周年”征文比赛,已知每篇参赛征文成绩记m分(60≤m≤100),组委会从1000篇征文中随机抽取了部分参赛征文,统计了他们的成绩,并绘制了如下不完整的两幅统计图表:
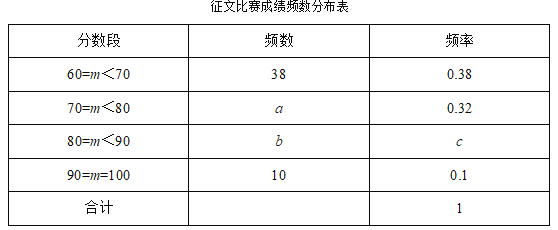
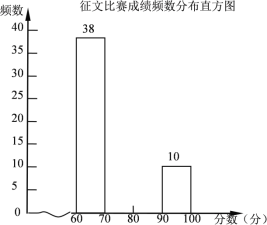
请根据以上信息,解决下列问题:
(1)征文比赛成绩频数分布表中c的值是________;
(2)补全征文比赛成绩频数分布直方图;
(3)若80分以上(含80分)的征文将被评为一等奖,试估计全市获得一等奖征文的篇数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知P是⊙O外一点,PO交⊙O于点C,OC=CP=4,弦AB⊥OC,劣弧AB的度数为120°,连接PB.
(1)求BC的长;
(2)求证:PB是⊙O的切线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有四个球,这四个球上分别标记数字﹣3、﹣1、0、2,除数字不同外,这四个球没有任何区别.
(1)从中任取一球,求该球上标记的数字为正数的概率;
(2)从中任取两球,将两球上标记的数字分别记为x、y,求点(x,y)位于第二象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某我市花石镇组织10辆汽车装运完A、B、C三种不同品质的湘莲共100吨到外地销售,按计划10辆汽车都要装满,且每辆汽车只能装同一种湘莲,根据下表提供的信息,解答以下问题:
(1)设装运A种湘莲的车辆数为x,装运B种湘莲的车辆数为y,求y与x之间的函数关系式;
(2)如果装运每种湘莲的车辆数都不少于2辆,那么车辆的安排方案有几种?并写出每种安排方案;
(3)若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润的值.
湘莲品种 | A | B | C |
每辆汽车运载量(吨) | 12 | 10 | 8 |
每吨湘莲获利(万元) | 3 | 4 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
平均数(分) | 中位数(分) | 众数(分) | |
初中部 | 85 | ||
高中部 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com