
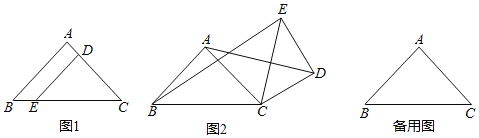
【题目】如图1,在Rt△ABC中,∠BAC=90°,AB=AC,D,E两点分别在AC,BC上,且DE∥AB,将△CDE绕点C按顺时针方向旋转,记旋转角为α.
(1)问题发现:当α=0°时,![]() 的值为 ;
的值为 ;
(2)拓展探究:当0°≤α<360°时,若△EDC旋转到如图2的情况时,求出![]() 的值;
的值;
(3)问题解决:当△EDC旋转至A,B,E三点共线时,若设CE=5,AC=4,直接写出线段BE的长 .
【答案】(1)![]() ;(2)
;(2)![]() ;(3)7或1.
;(3)7或1.
【解析】
(1)先证△DEC为等腰直角三角形,求出![]() ,再通过平行线分线段成比例的性质可直接写出
,再通过平行线分线段成比例的性质可直接写出![]() 的值;
的值;
(2)证△BCE∽△ACD,由相似三角形的性质可求出![]() 的值;
的值;
(3)分两种情况讨论,一种是点E在线段BA的延长线上,一种是点E在线段BA上,可分别通过勾股定理求出AE的长,即可写出线段BE的长.
(1)∵∠BAC=90°,AB=AC,
∴△ABC为等腰直角三角形,∠B=45°.
∵DE∥AB,
∴∠DEC=∠B=45°,∠CDE=∠A=90°,
∴△DEC为等腰直角三角形,
∴cos∠C![]() .
.
∵DE∥AB,
∴![]() .
.
故答案为:![]() ;
;
(2)由(1)知,△BAC和△CDE均为等腰直角三角形,
∴![]() .
.
又∵∠BCE=∠ACD=α,
∴△BCE∽△ACD,
∴![]() ,
,
即![]() ;
;
(3)①如图3﹣1,当点E在线段BA的延长线上时.
∵∠BAC=90°,
∴∠CAE=90°,
∴AE![]() 3,
3,
∴BE=BA+AE=4+3=7;
②如图3﹣2,当点E在线段BA上时,
AE![]() 3,
3,
∴BE=BA﹣AE=4﹣3=1.
综上所述:BE的长为7或1.
故答案为:7或1.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
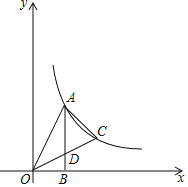
【题目】如图,在平面直角坐标系中,点O为坐标原点,直角三角形AOB的直角顶点B在x轴正半轴上,点A在第一象限,OB=2,tan∠AOB=2.
(1)求图象经过点A的反比例函数的解析式;
(2)点C是(1)中反比例函数图象上一点,连接OC交AB于点D,连接AC,若D为OC中点,求△ADC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形 OAA1B1 是边长为 1 的正方形,以对角线 OA1 为边作第二个正方形 OA1A2B2,连接 AA2,得到△ AA1A2;再以对角线 OA2 为边作第三个正方形 OA2A3B3,连接 A1A3,得到△A1A2A3;再以对角线 OA3 为边作第 四个正方形,连接 A2A4,得到△A2A3A4……记△AA1A2、△A1A2A3、△A2A3A4 的面积分别为 S1、S2、S3,如此下 去,则 S2019=_____ .
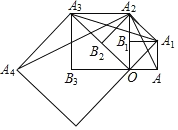
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,已知⊙O是△ABC的外接圆,AB为⊙O的直径,AC=6cm,BC=8cm.
(1)求⊙O的半径;
(2)请用尺规作图作出点P,使得点P在优弧CAB上时,△PBC的面积最大,请保留作图痕迹,并求出△PBC面积的最大值.
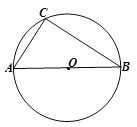
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C、D在⊙O上,连接AD、BC、BD、DC,若BD = CD,∠DBC = 20°,则,∠ABC =_________
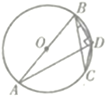
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,点
中,点![]() 是对角线
是对角线![]() 的中点,
的中点,![]() 是线段
是线段![]() 上的动点(不与点
上的动点(不与点![]() ,
,![]() 重合),
重合),![]() 交
交![]() 于点
于点![]() ,
,![]() 于点
于点![]() .则对于下列结论:①
.则对于下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中错误结论的个数是( )
,其中错误结论的个数是( )
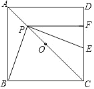
A.0B.1C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O直径,D为⊙O上一点,AT平分∠BAD交⊙O于点T,过T作AD的垂线交AD的延长线于点C.
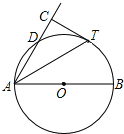
(1)求证:CT为⊙O的切线;
(2)若⊙O半径为2,CT=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com