
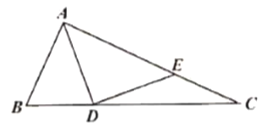
【题目】如图,![]() 是
是![]() 的角平分线,
的角平分线,![]() 在
在![]() 上,
上,![]() ,若
,若![]() ,
,![]() ,
,![]() ,则
,则![]() ________________.
________________.
【答案】![]()
【解析】
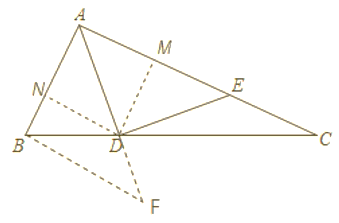
过点D作DM⊥AC于点M,作DN⊥AB于点N,设CM=![]() ,表示出CD和DM,再证明Rt△AMD≌Rt△AND,根据AB+CE=7,列出等式解出x,过点B作AC的平行线交AD延长线于点F,证明△BFD∽△CAD,从而求出AE长.
,表示出CD和DM,再证明Rt△AMD≌Rt△AND,根据AB+CE=7,列出等式解出x,过点B作AC的平行线交AD延长线于点F,证明△BFD∽△CAD,从而求出AE长.
过点D作DM⊥AC于点M,作DN⊥AB于点N,如图,
设CM=![]() ,
,
∵![]() ,
,
∴CD=7x,
∴![]() ,
,
∵AD平分∠BAC,
∴DN=DM=3x,
∵BD=3,
∴![]() ,
,
∵AD=DE,
∴![]() ,
,
在Rt△AMD和Rt△AND中,
![]()
∴Rt△AMD≌Rt△AND(HL),
∴AM=AN,
∴AN=EM,
∵AB+CE=7,
∴BN+AN+CE=7,
∴BN+EM+CE=7,
∴BN+CM=7,
∴BN=7-CM,
∴![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴CD=![]() ,
,![]() ,
,![]() ,
,
过点B作AC的平行线交AD延长线于点F,
则∠F=∠CAD,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴∠BAD=∠F,
∴BF=AB,
∵BF∥AC,
∴△BFD∽△CAD,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
设AN=AM=y,则AB=AN+BN=![]() ,
,
AC=AM+CM=![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴AE=2y![]() ,
,
故答案为:![]() .
.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以点M(0,![]() )为圆心,以
)为圆心,以![]() 长为半径作M交x轴于A.B两点,交y轴于C.D两点,连接AM并延长交M于P点,连接PC交x轴于E.
长为半径作M交x轴于A.B两点,交y轴于C.D两点,连接AM并延长交M于P点,连接PC交x轴于E.
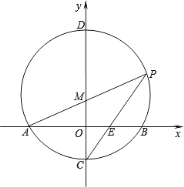
(1)求点C.P的坐标;
(2)求证:BE=2OE.
查看答案和解析>>
科目:初中数学 来源: 题型:
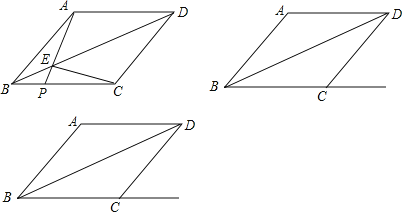
【题目】如图,菱形ABCD中,AB=10,连接BD,点P是射线BC上一点(不与点B重合),AP与对角线BD交于点E,连接EC.
(1)求证:AE=CE;
(2)若sin∠ABD=![]() ,当点P在线段BC上时,若BP=4,求△PEC的面积;
,当点P在线段BC上时,若BP=4,求△PEC的面积;
(3)若∠ABC=45°,当点P在线段BC的延长线上时,请直接写出△PEC是等腰三角形时BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
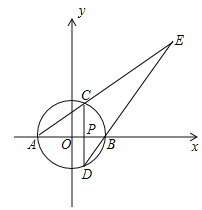
【题目】如图,以原点O为圆心,3为半径的圆与x轴分别交于A,B两点(点B在点A的右边),P是半径OB上一点,过P且垂直于AB的直线与⊙O分别交于C,D两点(点C在点D的上方),直线AC,DB交于点E.若AC:CE=1:2.
(1)求点P的坐标;
(2)求过点A和点E,且顶点在直线CD上的抛物线的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
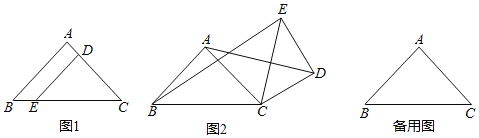
【题目】如图1,在Rt△ABC中,∠BAC=90°,AB=AC,D,E两点分别在AC,BC上,且DE∥AB,将△CDE绕点C按顺时针方向旋转,记旋转角为α.
(1)问题发现:当α=0°时,![]() 的值为 ;
的值为 ;
(2)拓展探究:当0°≤α<360°时,若△EDC旋转到如图2的情况时,求出![]() 的值;
的值;
(3)问题解决:当△EDC旋转至A,B,E三点共线时,若设CE=5,AC=4,直接写出线段BE的长 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 为直径,弦
为直径,弦![]() 交
交![]() 于点
于点![]() 、
、![]() ,连接
,连接![]() 、
、![]() ,
,![]() .
.
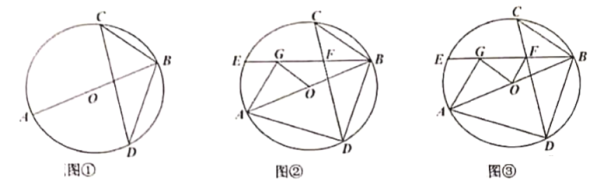
(1)如图①,求![]() 的度数;
的度数;
(2)如图②,弦![]() 交
交![]() 于点
于点![]() .在
.在![]() 上取点
上取点![]() ,连接
,连接![]() 、
、![]() 和
和![]() ,使
,使![]() ,求证:
,求证:![]() ;
;
(3)如图③,在(2)的条件下,![]() ,
,![]() 的直径为
的直径为![]() ,连接
,连接![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对于线段![]() 和点
和点![]() ,当
,当![]() ,且
,且![]() 时,称点
时,称点![]() 为线段
为线段![]() 的“等距点”.特别地,当
的“等距点”.特别地,当![]() ,且
,且![]() 时,称点
时,称点![]() 为线段
为线段![]() 的“强等距点”.在平面直角坐标系
的“强等距点”.在平面直角坐标系![]() 中,点
中,点![]() 的坐标为
的坐标为![]() .
.
(1)有4个点:![]() ,
,![]() ,
,![]() ,
,![]() .线段
.线段![]() 的“等距点”是 ;其中线段
的“等距点”是 ;其中线段![]() 的“强等距点”是 .
的“强等距点”是 .
(2)设第四象限有一点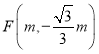 ,点
,点![]() 是线段
是线段![]() 的“强等距点”.
的“强等距点”.
①当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
②当点![]() 又为线段
又为线段![]() 的“等距点”时,求
的“等距点”时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 边上,点
边上,点![]() 在
在![]() 边上,
边上,![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
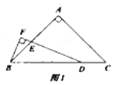
(1)如图1,当![]() 时:①
时:①![]() 的度数为__________;②求证;
的度数为__________;②求证;![]() ;
;
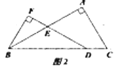
(2)如图2,当![]() 时,求
时,求![]() 的值(用含
的值(用含![]() 的式子表示).
的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
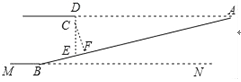
【题目】为缓解交通压力,市郊某地正在修建地铁站,拟同步修建地下停车库.如图是停车库坡道入口的设计图,其中MN是水平线,MN∥AD,AD⊥DE,CF⊥AB,垂足分别为D,F,坡道AB的坡度=1:3,AD=9米,点C在DE上,CD=0.5米,CD是限高标志牌的高度(标志牌上写有:限高 米).如果进入该车库车辆的高度不能超过线段CF的长,则该停车库限高多少米?(结果精确到0.1米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈3.16)
≈3.16)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com