
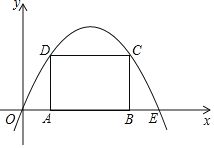
����Ŀ����ͼ��������y=ax2+bx��a��0������E��10��0��������ABCD�ı�AB���߶�OE�ϣ���A�ڵ�B����ߣ�����C��D���������ϣ���A��t��0������t=2ʱ��AD=4��
��1���������ߵĺ�������ʽ��
��2����tΪ��ֵʱ������ABCD���ܳ������ֵ�����ֵ�Ƕ��٣�
��3������t=2ʱ�ľ���ABCD����������ƽ�������ߣ���ƽ�ƺ������������εı�����������G��H����ֱ��GHƽ�־��ε����ʱ����������ƽ�Ƶľ��룮
���𰸡���1�������ߵĺ�������ʽΪy=��![]() x2+
x2+![]() x����2����t=1ʱ������ABCD���ܳ������ֵ�����ֵΪ
x����2����t=1ʱ������ABCD���ܳ������ֵ�����ֵΪ![]() ����3������������ƽ�Ƶľ�����4����λ��
����3������������ƽ�Ƶľ�����4����λ��
����������1���ɵ�E�������������ߵĽ���ʽ���ٰѵ�D�����꣨2��4���������ɵã�
��2���������ߵĶԳ��Ե�BE=OA=t���ݴ�֪AB=10-2t������x=tʱAD=-![]() t2+
t2+![]() t�����ݾ��ε��ܳ���ʽ�г���������ʽ���䷽�ɶ���ʽ���ɵã�
t�����ݾ��ε��ܳ���ʽ�г���������ʽ���䷽�ɶ���ʽ���ɵã�
��3����t=2�ó���A��B��C��D���Խ��߽���P�����꣬��ֱ��GHƽ�־��ε����ֱ֪��GH�ع���P������AB��CD֪�߶�ODƽ�ƺ�õ����߶���GH�����߶�OD���е�Qƽ�ƺ�Ķ�Ӧ����P֪PQ����OBD��λ�ߣ��ݴ˿ɵã�
��1���������߽���ʽΪy=ax��x-10����
�ߵ�t=2ʱ��AD=4��
���D��������2��4����
�ཫ��D����������ʽ��-16a=4��
��ã�a=-![]() ��
��
�����ߵĺ�������ʽΪy=-![]() x2+
x2+![]() x��
x��
��2���������ߵĶԳ��Ե�BE=OA=t��
��AB=10-2t��
��x=tʱ��AD=-![]() t2+
t2+![]() t��
t��
�����ABCD���ܳ�=2��AB+AD��
=2[��10-2t��+��-![]() t2+
t2+![]() t��]
t��]
=-![]() t2+t+20
t2+t+20
=-![]() ��t-1��2+
��t-1��2+![]() ��
��
��-![]() ��0��
��0��
�൱t=1ʱ������ABCD���ܳ������ֵ�����ֵΪ![]() ��
��
��3����ͼ��

��t=2ʱ����A��B��C��D������ֱ�Ϊ��2��0������8��0������8��4������2��4����
�����ABCD�Խ��ߵĽ���P������Ϊ��5��2����
��ƽ�ƺ�������߹���Aʱ����H������Ϊ��4��4������ʱGH���ܽ��������ƽ�֣�
��ƽ�ƺ�������߹���Cʱ����G������Ϊ��6��0������ʱGHҲ���ܽ��������ƽ�֣�
�൱G��H����һ�������߶�AD��BC��ʱ��ֱ��GH�����ܽ����ε����ƽ�֣�
����G��H�ֱ������߶�AB��DC��ʱ��ֱ��GH����P��ƽ�־���ABCD�������
��AB��CD��
���߶�ODƽ�ƺ�õ����߶�GH��
���߶�OD���е�Qƽ�ƺ�Ķ�Ӧ����P��
����OBD�У�PQ����λ�ߣ�
��PQ=![]() OB=4��
OB=4��
��������������ƽ�Ƶľ�����4����λ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����ϵ�A��B��C����ʾ�����ֱ��ǩ�2��+8��x��AC��6��
��1���������Ტ�����A��B��λ�ã�
��2��ȷ��x��ֵΪ�� ����
��3������M��N�ֱ���AB��AC���е㣬���߶�MN�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳�Ϊ1��AC��BD�ǶԽ��ߣ�����DCB���ŵ�D˳ʱ����ת45���õ���DGH��HG��AB�ڵ�E������DE��AC�ڵ�F������FG�������н��ۣ�
���ı���AEGF�����ڡ�AED�ա�GED�ۡ�DFG=112.5����BC+FG=1.5������ȷ�Ľ�����________��

�鿴�𰸺ͽ���>>
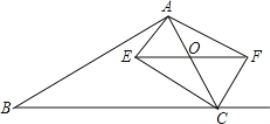
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���O��AC����һ���㣬����O��BC��ƽ���߽���ACB�Ľ�ƽ�����ڵ�E������ACB�����ƽ�����ڵ�F
(1)��֤��EO=FO��
(2)����O�˶����δ�ʱ���ı���CEAF�Ǿ���?��֤����Ľ��ۡ�
(3)�ڵ�(2)�ʵĽ����£���AE=3��EC=4��AB=12��BC=13����������ı���ABCE�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
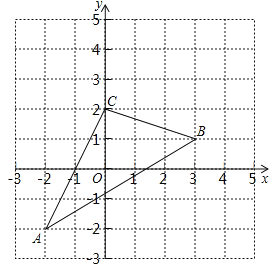
����Ŀ����ͼ����ABC��ֱ������ϵ�У�
��1�����ѡ�ABC����ƽ��2����λ��������ƽ��1����λ�õ���A1B1C1��������A1B1C1����д����A1��B1��C1�����ꣻ
��2�����ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Ӽص��ҵ���ȥ���������͵�![]() �����ҵص�������ȥʣ�����͵�
�����ҵص�������ȥʣ�����͵�![]() �������л�ʣ6�����ͣ�������ء��ҵء����ء�������ͬһֱ���ϣ��Ұ�����˳��ֲ�����
�������л�ʣ6�����ͣ�������ء��ҵء����ء�������ͬһֱ���ϣ��Ұ�����˳��ֲ�����
��1����������ԭ�����Ͷ�������
��2�����ס����������22ǧ�ף����ҡ�����������Զ������������ʻ��������ʻ��·��������������ȣ���
��3���ڣ�2���������£������ؾ����10ǧ�ף��������ڲ����͵�����£��ܷ�ȥ���أ�Ȼ������ԭ·���ص��أ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ijѧУ�������飬A��ѧ���ﹲ��������B��ѧ������������˽�ҳ��ȣ�C��ѧ�����У�D��ѧ���������������ݵ����������˲�������ͳ��ͼ��
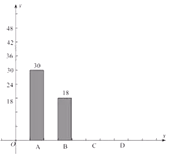
���� | Ƶ�� | Ƶ�� |
A | 30 |
|
B | 18 | 0.15 |
C |
| 0.40 |
D |
|
|
��1��ѧ����________�ˣ� ![]() ________��
________�� ![]() ________��
________��
��2����ȫ����ͳ��ͼ��
��3������У����2000�ˣ��ﹲ����������________�ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������OA�ķ����DZ�ƫ��20��������OB�ķ����DZ�ƫ��40����OD��OB�ķ����ӳ��ߣ�OC�ǡ�AOD��ƽ���ߡ�
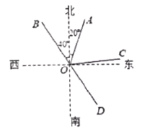
��1�����DOC�Ķ�����
��2���������OC�ķ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ�����ǰ�ABC��ֱ�Ƕ���C��ֱ��DE�ϣ�CFƽ�֡�BCD��
��1����ͼ1�У�����BCE=40�������ACF�Ķ�����
��2����ͼ1�У�����BCE=����ֱ��д����ACF�Ķ������ú�����ʽ�ӱ�ʾ����
��3����ͼ1�е����ǰ�ABC�ƶ���C��ת��ͼ2��λ�ã�̽����д����ACF���BCE�Ķ���֮��Ĺ�ϵ����˵�����ɣ�
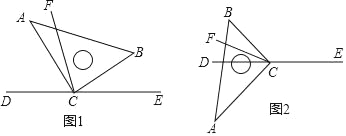
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com