
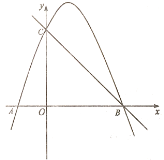
【题目】如图,抛物线![]() 与x轴交于点
与x轴交于点![]() ,B两点,与y轴交于点
,B两点,与y轴交于点![]() ,抛物线的顶点在直线
,抛物线的顶点在直线![]() 上.
上.
(1)求抛物线的解析式;
(2)点P为第一象限内抛物线上的一个动点,过点P做![]() 轴交BC于点Q,求线段PQ长度的最大值,及此时点P的坐标;
轴交BC于点Q,求线段PQ长度的最大值,及此时点P的坐标;
(3)点M在x轴上,点N在抛物线的对称轴上,若以点M,N,C,B为顶点的四边形是平行四边形,请直接写出点M的坐标.
【答案】(1)![]() ;(2)PQ长度的最大值为
;(2)PQ长度的最大值为![]() ,点P的坐标为
,点P的坐标为![]() ;(3)点M的坐标为
;(3)点M的坐标为![]() ,
,![]() ,
,![]() .
.
【解析】
(1)根据对称轴为直线x=1,和点A坐标可知点B坐标,由点A,B,C的坐标,利用待定系数法即可求出抛物线的解析式;
(2)先求出过B,C两点的直线解析式,之后即可设出![]() ,
,![]() ,再根据两点之间的距离公式,即可得出
,再根据两点之间的距离公式,即可得出![]() ,化成顶点式即可求出答案;
,化成顶点式即可求出答案;
(3)设点M的坐标为(m,0),点N的坐标为(1,n).分四边形CBMN为平行四边形,四边形CMBN为平行四边形,四边形CMBN为平行四边形三种情况,利用平行四边形的性质找出关于m的一元一次方程,解答即可得出答案.
解(1)∵对称轴为直线x=1,点A坐标为(-1,0),
∴点B坐标为(3,0)
将A(-1,0),B(3,0),C(0,3)代入![]() 中有:
中有:
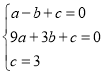 ,
,
解得:
∴抛物线解析式为:![]() .
.
(2)设过B,C两点的直线解析式为![]()
将B(3,0),C(0,3)代入解得b=3,k=-1,
∴直线BC的解析式为![]() .
.
设点![]() ,
,![]() .
.
∴![]() .
.
∴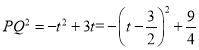
∴当![]() 时,
时,![]() 长度的最大值为
长度的最大值为![]() .
.
此时,![]() .
.
∴点P的坐标为![]() .
.
(3)设点M的坐标为(m,0),点N的坐标为(1,n).分三种情况考虑:
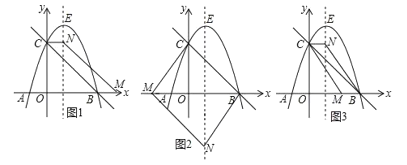
①如图1,当四边形CBMN为平行四边形时,有1-0=m-3,解得m=4,
所以此时点M的坐标为(4,0)
②如图2,当四边形CMBN为平行四边形时,有m-1=0-3,解得m=-2,
所以此时点M的坐标为(-2,0)
③如图3,当四边形CMBN为平行四边形时,有0-1=m-3,解得m=2,
所以此时点M的坐标为(2,0);
综上,点M的坐标为![]() ,
,![]() ,
,![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】我市茶叶专卖店销售某品牌茶叶,其进价为每千克 240 元,按每千克 400 元出售,平均每周可售出 200 千克,后来经过市场调查发现,单价每降低 10 元,则平均每周的销售量可增加 40 千克,若该专卖店销售这种品牌茶叶要想平均每周获利 41600 元,请回答:
(1)每千克茶叶应降价多少元?
(2)在平均每周获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的 几折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义两个不相交的函数图象在竖直方向上的最短距离为这两个函数的“和谐值”.
(1)求抛物线y=x2﹣2x+2与x轴的“和谐值”;
(2)求抛物线y=x2﹣2x+2与直线y=x﹣1的“和谐值”.
查看答案和解析>>
科目:初中数学 来源: 题型:
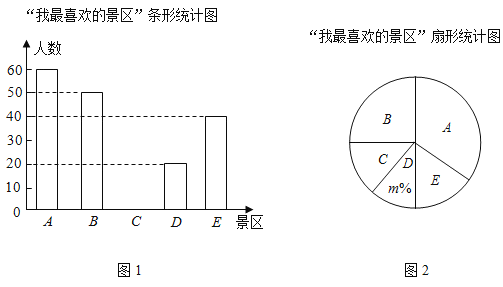
【题目】“活力新衢州,美丽大花园”.衢州市某中学九年级开展了“我最喜爱的旅游景区”的抽样调查(每人只能选一项):A﹣“世界文化新遗产”开化根博园;B﹣“首个自然遗产”江郎山;C﹣“乌溪江上的明珠”九龙湖;D﹣“世界最大的象形石动物园”三衢石林;E﹣“世界第九大奇迹”龙游石窟.根据收集的数据绘制了两幅不完整的统计图,其中B对应的圆心角为90°.请根据图中信息解答下列问题:
(1)此次抽取的九年级学生共 人,并补全条形统计图;
(2)扇形统计图中m= ,表示E的扇形的圆心角是 度;
(3)九年级准备在最喜爱A景区的4名优秀学生中任意选择两人去实地考察,这4名学生中有2名男生和2名女生,用树状图或列表法求选出的两名学生都是男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批衬衫,平均每天可售出20件,每件盈利40元,经过调查发现,销售单价每降低5元,每天可多售出10件,下列说法错误的是( )
A.销售单价降低15元时,每天获得利润最大
B.每天的最大利润为1250元
C.若销售单价降低10元,每天的利润为1200元
D.若每天的利润为1050元,则销售单价一定降低了5元
查看答案和解析>>
科目:初中数学 来源: 题型:
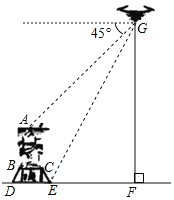
【题目】为了测量重庆有名的观景点南山大金鹰的大致高度,小南同学使用的无人机进行观察,当无人机与大金鹰侧面在同一平面,且距离水平面垂直高度GF为100米时,小南调整摄像头方向,当俯角为45°时,恰好可以拍摄到金鹰的头顶A点;当俯角为63°时,恰好可以拍摄到金鹰底座点E.已知大金鹰是雄踞在一人造石台上,石台侧面CE长12.5米,坡度为1:0.75,石台上方BC长10米,头部A点位于BC中点正上方.则金鹰自身高度约( )米.(结果保留一位小数,sin63°≈0.89,cos63°≈0.45,tan63°≈1.96)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两工程队共同承建某高速路隧道工程,隧道总长2000米,甲、乙分别从隧道两端向中间施工,计划每天各施工6米.因地质情况不同,两支队伍每合格完成1米隧道施工所需成本不一样.甲每合格完成1米,隧道施工成本为6万元;乙每合格完成1米,隧道施工成本为8万元.
(1)若工程结算时乙总施工成本不低于甲总施工成本的![]() ,求甲最多施工多少米?
,求甲最多施工多少米?
(2)实际施工开始后因地质情况比预估更复杂,甲乙两队每日完成量和成本都发生变化.甲每合格完成1米隧道施工成本增加m万元时,则每天可多挖![]() m米,乙因特殊地质,在施工成本不变的情况下,比计划每天少挖
m米,乙因特殊地质,在施工成本不变的情况下,比计划每天少挖![]() m米,若最终每天实际总成本比计划多(11m-8)万元,求m的值.
m米,若最终每天实际总成本比计划多(11m-8)万元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的方法解方程。
(1)4(x-3) ![]() =36
=36
(2)x2-4x+1=0.
(3)![]() -7x+6=0
-7x+6=0
(4)![]()
(5)(y-1)2+2y(1-y)=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学复习课上,数学老师用几何画板上画出二次函数y=ax2+bx+c(a≠0)图象如图所示,四名同学根据图象,说出下列结论:李佳:abc<0:王宁:2a﹣b<0:孙浩:b2>4ac一帆:点(﹣3,y1),(1,y2)都在抛物线上,则有y1>y2,你认为其中正确的结论有( )
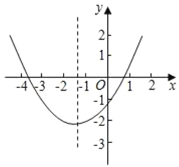
A.4个B.3个C.2个D.1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com