
【题目】某数学复习课上,数学老师用几何画板上画出二次函数y=ax2+bx+c(a≠0)图象如图所示,四名同学根据图象,说出下列结论:李佳:abc<0:王宁:2a﹣b<0:孙浩:b2>4ac一帆:点(﹣3,y1),(1,y2)都在抛物线上,则有y1>y2,你认为其中正确的结论有( )
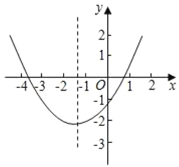
A.4个B.3个C.2个D.1个
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:初中数学 来源: 题型:
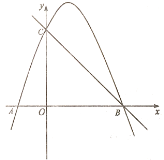
【题目】如图,抛物线![]() 与x轴交于点
与x轴交于点![]() ,B两点,与y轴交于点
,B两点,与y轴交于点![]() ,抛物线的顶点在直线
,抛物线的顶点在直线![]() 上.
上.
(1)求抛物线的解析式;
(2)点P为第一象限内抛物线上的一个动点,过点P做![]() 轴交BC于点Q,求线段PQ长度的最大值,及此时点P的坐标;
轴交BC于点Q,求线段PQ长度的最大值,及此时点P的坐标;
(3)点M在x轴上,点N在抛物线的对称轴上,若以点M,N,C,B为顶点的四边形是平行四边形,请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践探究几何元素之间的关系
问题情境:四边形ABCD中,点O是对角线AC的中点,点E是直线AC上的一个动点(点E与点C,O,A都不重合),过点A,C分别作直线BE的垂线,垂足分别为F,G,连接OF,OG.
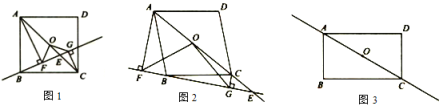
(1)初步探究:
如图1,已知四边形ABCD是正方形,且点E在线段OC上,求证![]() ;
;
(2)深入思考:请从下面A,B两题中任选一题作答,我选择_______题.
A.探究图1中OF与OG的数量关系并说明理由;
B.如图2,已知四边形ABCD为菱形,且点E在AC的延长线上,其余条件不变,探究OF与OG的数量关系并说明理由;
(3)拓展延伸:请从下面AB两题中任选一题作答,我选择_______题.
如图3,已知四边形ABCD为矩形,且![]() ,
,![]() .
.
A.点E在直线AC上运动的过程中,若![]() ,则FG的长为________.
,则FG的长为________.
B.点E在直线AC上运动的过程中,若![]() ,则FG的长为________.
,则FG的长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽和小华想利用摸球游戏决定谁去参加市里举办的书法比赛,游戏规则是:在一个不透明的袋子里装有除数字外完全相同的4个小球,上面分别标有数字2,3,4,5.一人先从袋中随机摸出一个小球,另一人再从袋中剩下的3个小球中随机摸出一个小球.若摸出的两个小球上的数字和为偶数,则小丽去参赛;否则小华去参赛.
(1)用列表法或画树状图法,求小丽参赛的概率.
(2)你认为这个游戏公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
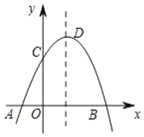
【题目】如图,抛物线y=﹣x2+2x+3交x轴于A,B两点,交y轴于点C,点D为抛物线的顶点,点C关于抛物线的对称轴的对称点为E,点G,F分别在x轴和y轴上,则四边形EDFG周长的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
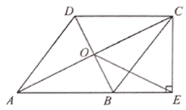
(1)求证:四边形ABCD是菱形;(2)若AE=5,OE=3,求线段CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标平面xOy内,点A(6,0)、C(﹣4,0),过点A作直线AB,交y轴的正半轴于点B,且AB=10,点P是直线AB上的一个动点.
(1)求点B的坐标和直线AB的表达式;
(2)若以A、P、C为顶点的三角形与△AOB相似,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湘潭市继2017年成功创建全国文明城市之后,又准备争创全国卫生城市.某小区积极响应,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买2个温馨提示牌和3个垃圾箱共需550元,且垃圾箱的单价是温馨提示牌单价的3倍.
(1)求温馨提示牌和垃圾箱的单价各是多少元?
(2)该小区至少需要安放48个垃圾箱,如果购买温馨提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com