
【题目】综合与实践探究几何元素之间的关系
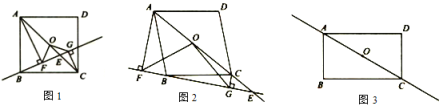
问题情境:四边形ABCD中,点O是对角线AC的中点,点E是直线AC上的一个动点(点E与点C,O,A都不重合),过点A,C分别作直线BE的垂线,垂足分别为F,G,连接OF,OG.
(1)初步探究:
如图1,已知四边形ABCD是正方形,且点E在线段OC上,求证![]() ;
;
(2)深入思考:请从下面A,B两题中任选一题作答,我选择_______题.
A.探究图1中OF与OG的数量关系并说明理由;
B.如图2,已知四边形ABCD为菱形,且点E在AC的延长线上,其余条件不变,探究OF与OG的数量关系并说明理由;
(3)拓展延伸:请从下面AB两题中任选一题作答,我选择_______题.
如图3,已知四边形ABCD为矩形,且![]() ,
,![]() .
.
A.点E在直线AC上运动的过程中,若![]() ,则FG的长为________.
,则FG的长为________.
B.点E在直线AC上运动的过程中,若![]() ,则FG的长为________.
,则FG的长为________.
【答案】(1)见解析;(2)A. ![]() ,理由见解析;B.
,理由见解析;B. ![]() . 理由见解析;(3)A.
. 理由见解析;(3)A.![]() B.
B.![]() 或
或![]()
【解析】
(1)根据题意,AF⊥BE,CG⊥BE,![]() ,
,![]() ,则
,则![]() ,利用AAS证明
,利用AAS证明![]() ,即可得到答案;
,即可得到答案;
(2)A.由(1)知![]() ,
,![]() ,然后得到OB=OA,由
,然后得到OB=OA,由![]() ,得到
,得到![]() ,即可得到OF=OG;
,即可得到OF=OG;
B.延长GO交FA的延长线于点H,找到条件,证明![]() ,然后得到OH=OG=OF;
,然后得到OH=OG=OF;
(3)A.根据矩形的性质,得到△ABO是等边三角形,然后得到∠ABF=30°,则![]() ,由勾股定理,求出BF和BG的长度,即可得到FG.
,由勾股定理,求出BF和BG的长度,即可得到FG.
B.根据题意,由![]() ,由两种情况,要进行分类讨论;结合矩形的性质,得到△AFB和△BCG是等腰直角三角形,利用三角函数值,求出BF和BG的长度,然后求出FG的长度即可.
,由两种情况,要进行分类讨论;结合矩形的性质,得到△AFB和△BCG是等腰直角三角形,利用三角函数值,求出BF和BG的长度,然后求出FG的长度即可.
(1)证明:∵四边形ABCD是正方形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)A.解:![]() ;
;
理由如下:如图1,连接OB,

由(1)知![]() ,
,![]() ,
,![]() ,
,
∵点O是AC的中点,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
B.解:![]() .
.
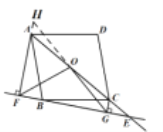
理由如下:延长GO交FA的延长线于点H,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵点O是AC的中点,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3)A、解:如图:连接OB,
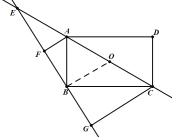
在直角三角形ABC中,OA=OB=OC,
∵∠BAC=60°,
∴△ABO是等边三角形,
∴∠ABO=60°,
∵BF=BG,
∴点B是FG的中点,
∴OB∥AF,
∴∠BAF=60°,
∵∠AFB=90°,
∴∠ABF=30°,
∴![]() ,
,
∴![]() ,
,
∴BG=![]() ,
,
∴FG=![]() ;
;
故答案为:![]() .
.
B.解:①如图,OF∥BC,则OF⊥AB,
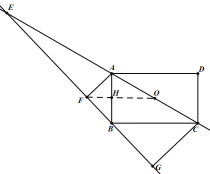
∵点O为AC中点,
∴点H为AB的中点,即AH=BH,
∴△ABF是等腰三角形,则AF=BF,
∵∠AFB=90°,
∴∠BAF=∠ABF=45°,
∴![]() ,
,
同理:△BCG是等腰直角三角形,![]() ,
,
∴![]() ,
,
∴![]() ;
;
②如图,OF∥BC,延长OF交AB于点I,
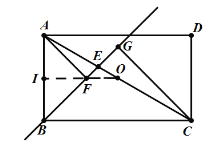
由①可知,△ABF是等腰直角三角形,![]() ,
,
△BCG是等腰直角三角形,![]() ,
,
∴![]() ;
;
综合上述,FG的长度为:![]() 或
或![]() .
.
故答案为:![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】我们定义两个不相交的函数图象在竖直方向上的最短距离为这两个函数的“和谐值”.
(1)求抛物线y=x2﹣2x+2与x轴的“和谐值”;
(2)求抛物线y=x2﹣2x+2与直线y=x﹣1的“和谐值”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两工程队共同承建某高速路隧道工程,隧道总长2000米,甲、乙分别从隧道两端向中间施工,计划每天各施工6米.因地质情况不同,两支队伍每合格完成1米隧道施工所需成本不一样.甲每合格完成1米,隧道施工成本为6万元;乙每合格完成1米,隧道施工成本为8万元.
(1)若工程结算时乙总施工成本不低于甲总施工成本的![]() ,求甲最多施工多少米?
,求甲最多施工多少米?
(2)实际施工开始后因地质情况比预估更复杂,甲乙两队每日完成量和成本都发生变化.甲每合格完成1米隧道施工成本增加m万元时,则每天可多挖![]() m米,乙因特殊地质,在施工成本不变的情况下,比计划每天少挖
m米,乙因特殊地质,在施工成本不变的情况下,比计划每天少挖![]() m米,若最终每天实际总成本比计划多(11m-8)万元,求m的值.
m米,若最终每天实际总成本比计划多(11m-8)万元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的方法解方程。
(1)4(x-3) ![]() =36
=36
(2)x2-4x+1=0.
(3)![]() -7x+6=0
-7x+6=0
(4)![]()
(5)(y-1)2+2y(1-y)=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“共和国勋章”是中华人民共和国的最高荣誉勋章.在2019年获得“共和国勋章”的八位杰出人物中,有于敏、孙家栋、袁隆平、黄旭华四位院士.如图是四位院士(依次记为A,B,C,D)为让同学们了解四位院士的贡献,老师设计如下活动:取四张完全相同的卡片,分别写上A,B,C,D四个标号,然后背面朝上放置,搅匀后每个同学可从中随机抽取一张,记下标号后放回,老师要求每位同学根据抽到的卡片上的标号查找相应院士的资料制作小报,求小明和小华查找同一位院士资料的概率.
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市以20元/千克的进货价购进了一批绿色食品,如果以30元/千克销售这些绿色食品,那么每天可售出400千克.由销售经验可知,每天的销售量y(千克)与销售单价x(元)(x≥30)存在如图所示的一次函数关系.
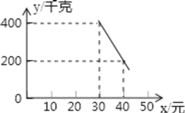
(1)试求出y与x的函数关系式;
(2)设该超市销售该绿色食品每天获得利润w元,当销售单价为何值时,每天可获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,甲、乙两人在玩转盘游戏时,分别把转盘A,B分成3等份和1等份,并在每一份内标上数字.游戏规则:同时转动两个转盘,当转盘停止后,指针所在区域的数字之积为奇数时,甲获胜;当数字之积为偶数时,乙获胜.如果指针恰好在分割线上时,则需重新转动转盘.
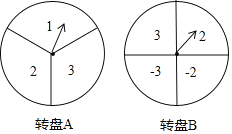
(1)利用画树状图或列表的方法,求甲获胜的概率.
(2)这个游戏规则对甲、乙双方公平吗?若公平,请说明理由;若不公平,请你在转盘A上只修改一个数字使游戏公平(不需要说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学复习课上,数学老师用几何画板上画出二次函数y=ax2+bx+c(a≠0)图象如图所示,四名同学根据图象,说出下列结论:李佳:abc<0:王宁:2a﹣b<0:孙浩:b2>4ac一帆:点(﹣3,y1),(1,y2)都在抛物线上,则有y1>y2,你认为其中正确的结论有( )
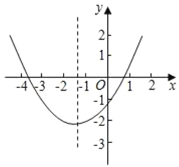
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利达经销店为某工厂代销一种建筑材料(这里的代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每下降10元时,月销售量就会增加7.5吨.综合考虑各种因素,每售出一吨建筑材料共需支付厂家及其它费用100元.
(1)当每吨售价是240元时,计算此时的月销售量;
(2)在遵循“薄利多销”的原则下,问每吨材料售价为多少时,该经销店的月利润为9000元?
(3)小静说:“当月利润最大时,月销售额也最大.”你认为对吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com