
����Ŀ��������ѫ�¡����л��������������ѫ��.��2019���á�����ѫ�¡��İ�λ�ܳ������У�����������Ҷ���Ԭ¡ƽ��������λԺʿ.��ͼ����λԺʿ�����μ�ΪA��B��C��D��Ϊ��ͬѧ���˽���λԺʿ�Ĺ��ף���ʦ������»��ȡ������ȫ��ͬ�Ŀ�Ƭ���ֱ�д��A��B��C��D�ĸ���ţ�Ȼ���泯�Ϸ��ã����Ⱥ�ÿ��ͬѧ�ɴ��������ȡһ�ţ����±�ź�Żأ���ʦҪ��ÿλͬѧ���ݳ鵽�Ŀ�Ƭ�ϵı�Ų�����ӦԺʿ����������С������С����С������ͬһλԺʿ���ϵĸ���.
A.  B.
B.  C.
C.  D.
D. 
���𰸡�![]() .
.
��������
�����������г����ó�����16�ֵȿ��ܵĽ�����������ø��ʹ�ʽ���ɵã�
�⣺���п��ܵĽ�����£�
�� �� | A | B | C | D |
A | ��A,A�� | ��A,B�� | ��A,C�� | ��A,D�� |
B | ��B,A�� | ��B,B�� | ��B,C | ��B,D�� |
C | ��C,A�� | ��C,B�� | ��C,C�� | ��C,D�� |
D | ��D,A�� | ��D,B�� | ��D,C�� | ��D,D�� |
�ɱ����֪��һ����16�ֽ����ÿ�ֽ�����ֵĿ����Զ���ͬ������С����С���鵽ͬһλԺʿ�Ľ����4�֣�
��![]() .
.


 Сѧѧϰ�ð���ϵ�д�
Сѧѧϰ�ð���ϵ�д� Сѧͬ�����������ܾ�ϵ�д�
Сѧͬ�����������ܾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y��ax2+bx+c�е�y��x�IJ��ֶ�Ӧֵ���±���
x | ��1 | 0 | 1 | 3 |
y | ��3 | 1 | 3 | 1 |
���н����У��������ߵĿ������£�����ͼ��ĶԳ���Ϊx��1������x��1ʱ������ֵy��x�����������������ax2+bx+c��0��һ��������4������ax12+bx1��ax22+bx2����x1��x2����x1+x2��3��������ȷ�Ľ�����(����)
A.�٢ڢ�B.�٢ڢۢܢ�C.�٢ۢ�D.�٢ۢܢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB=6��BC=8����OΪ�Խ���BD���е㣬��EΪ��AD��һ�㣬����OE������DOE��OE���۵õ���OEF����OF��AD�ڵ�G����OE=______��
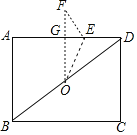
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y��ax2��bx��c�Ķ�������Ϊ��2��9������y�ύ�ڵ�A��0��5������x�ύ�ڵ�E��B.
��1������κ���y��ax2��bx��c�Ľ���ʽ.
��2������A��ACƽ����x�ᣬ���������ڵ�C����PΪ��������һ�㣨��P��AC�Ϸ�������PDƽ����y�ύAB�ڵ�D,�ʵ���P�ں�λ��ʱ���ı���APCD����������P���꼰�������Ƕ��٣�
��3������M���������ϣ���N����Գ����ϣ�ʹ����A��E��N��MΪ������ı�����ƽ���ı��Σ�ֱ��д��M������.
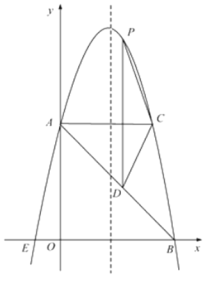
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���mx2��2x��1��0.
(1)������������ʵ��������m��ȡֵ��Χ��
(2)�����̵�����ʵ����Ϊx1��x2����x1x2��x1��x2��![]() ����m��ֵ��
����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���ʵ��̽������Ԫ��֮��Ĺ�ϵ
�����龳���ı���ABCD�У���O�ǶԽ���AC���е㣬��E��ֱ��AC�ϵ�һ�����㣨��E���C��O��A�����غϣ�������A��C�ֱ���ֱ��BE�Ĵ��ߣ�����ֱ�ΪF��G������OF��OG.
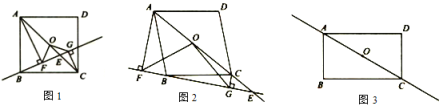
��1������̽����
��ͼ1����֪�ı���ABCD�������Σ��ҵ�E���߶�OC�ϣ���֤![]() ��
��
��2������˼�����������A��B��������ѡһ��������ѡ��_______��.
A.̽��ͼ1��OF��OG��������ϵ��˵�����ɣ�
B.��ͼ2����֪�ı���ABCDΪ���Σ��ҵ�E��AC���ӳ����ϣ������������䣬̽��OF��OG��������ϵ��˵�����ɣ�
��3����չ���죺�������AB��������ѡһ��������ѡ��_______��.
��ͼ3����֪�ı���ABCDΪ���Σ���![]() ��
��![]() .
.
A.��E��ֱ��AC���˶��Ĺ����У���![]() ����FG�ij�Ϊ________.
����FG�ij�Ϊ________.
B.��E��ֱ��AC���˶��Ĺ����У���![]() ����FG�ij�Ϊ________.
����FG�ij�Ϊ________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У���ADC��ƽ������AB����E����F��DE���ӳ����ϣ���BFE=90��������AF��CF��CF��AB����G�������½��ۣ�
��AE=BC
��AF=CF
��BF2=FGFC
��EGAE=BGAB
������ȷ�ĸ����ǣ�������
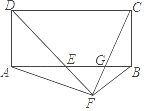
A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����С��������������Ϸ����˭ȥ�μ�����ٰ���鷨��������Ϸ�����ǣ���һ�������Ĵ�����װ�г���������ȫ��ͬ��4��С������ֱ��������2��3��4��5��һ���ȴӴ����������һ��С����һ���ٴӴ���ʣ�µ�3��С�����������һ��С��������������С���ϵ����ֺ�Ϊż������С��ȥ����������С��ȥ������
��1�����б�������״ͼ������С�������ĸ��ʣ�
��2������Ϊ�����Ϸ��ƽ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ�������ϣ����ش�����������⣮
�������ڽ�ƽ���߶����������ε��ڽ�ƽ���߷ֶԱ����õ������߶κ�����ǵ����߶�Ӧ�ɱ�����
��֪����ͼ����ABC�У�AD�ǽ�ƽ���ߣ�
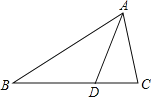
��֤��![]() ��
��
֤������C��CE��DA����BA���ӳ�����E��
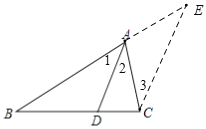
���1����E����2����3��
��AD�ǽ�ƽ���ߣ�
���1����2��
���3����E��
��AC��AE��
�֡�CE��DA��
��![]() ��������
��������
��![]() ��
��
(1)����֤�������У�����������������_____
(2)���������ڽ�ƽ���߶��������֪����ABC�У�AD�ǽ�ƽ���ߣ�AB��7cm��AC��4cm��BC��6cm����BD�ij�Ϊ_____cm��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com