
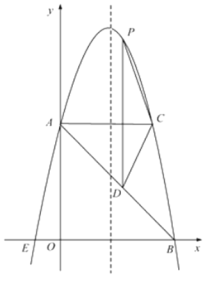
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y��ax2��bx��c�Ķ�������Ϊ��2��9������y�ύ�ڵ�A��0��5������x�ύ�ڵ�E��B.
��1������κ���y��ax2��bx��c�Ľ���ʽ.
��2������A��ACƽ����x�ᣬ���������ڵ�C����PΪ��������һ�㣨��P��AC�Ϸ�������PDƽ����y�ύAB�ڵ�D,�ʵ���P�ں�λ��ʱ���ı���APCD����������P���꼰�������Ƕ��٣�
��3������M���������ϣ���N����Գ����ϣ�ʹ����A��E��N��MΪ������ı�����ƽ���ı��Σ�ֱ��д��M������.
���𰸡���1��y����x2��4x��5,��2��![]() ,P��
,P��![]() ,
,![]() ��;��3��M1(3��8),M2(1��8).
��;��3��M1(3��8),M2(1��8).
��������
��1����������߽���ʽ���ô���ϵ������⼴�ɣ�
��2�������ֱ��AB����ʽ�������P���꣨x��x2��4x��5��������������ϵʽS�ı���APCD��2x2��10x�����ݶ��κ��������ֵ��
��3�����жϳ���HMN�ա�AOE�����M��ĺ����꣬�Ӷ������M�����꣮
��1���������߽���ʽΪy��a��x2��2��9��
����������y�ύ�ڵ�A��0��5����
��4a��9��5��
��a��1��
y����x2��2��9��x2��4x��5��
��2����y��0ʱ��x2��4x��5��0��
��x1��1��x2��5��
��E��1��0����B��5��0����
��ֱ��AB�Ľ���ʽΪy��mx��n��
��A��0��5����B��5��0����
��m��1��n��5��
��ֱ��AB�Ľ���ʽΪy��x��5��
��P��x��x2��4x��5����
��D��x��x��5����
��PD��x2��4x��5��x5��x2��5x��
��AC��4��
��S�ı���APCD��![]() ��AC��PD��2��x2��5x����2x2��10x��
��AC��PD��2��x2��5x����2x2��10x��
�൱x��![]() ʱ��S=
ʱ��S=![]() ��
��
�༴����P��![]() ��
��![]() ��ʱ��S�ı���APCD���
��ʱ��S�ı���APCD���![]() ��
��
��3����ͼ��
��M��MH��ֱ�ڶԳ��ᣬ����ΪH��
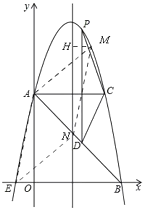
��MN��AE��MN��AE��
���HMN�ա�AOE
��HM��OE��1��
��M��ĺ�����Ϊx��3��x��1��
��x��1ʱ��M��������Ϊ8��
��x��3ʱ��M��������Ϊ8��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��������![]() ��
��![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��![]() ����
����![]() ���ڵ�
���ڵ�![]() .
.
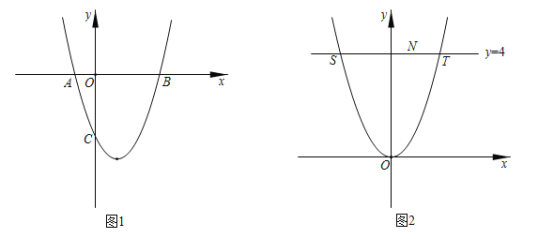
��1��ֱ��д����![]() ʱ��
ʱ��![]() ��ȡֵ��Χ��____________��
��ȡֵ��Χ��____________��
��2����![]() ��������
��������![]() �ϣ���
�ϣ���![]() �������
�������
��3����ͼ2����������![]() ƽ�ƣ�ʹ�䶥��Ϊԭ��
ƽ�ƣ�ʹ�䶥��Ϊԭ��![]() ���õ�������
���õ�������![]() ��ֱ��
��ֱ��![]() ��������
��������![]() ����
����![]() ��
��![]() ���㣬��
���㣬��![]() ���߶�
���߶�![]() ��һ���㣨����
��һ���㣨����![]() ��
��![]() �غϣ�����̽��������
�غϣ�����̽��������![]() ���Ƿ���ڵ�
���Ƿ���ڵ�![]() ����
����![]() ���ڵ�
���ڵ�![]() �����ĶԳƵ�
�����ĶԳƵ�![]() Ҳ��������
Ҳ��������![]() ��.
��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����һ��������ƽ��ÿ����۳�20����ÿ��ӯ��40Ԫ���������鷢�֣����۵���ÿ����5Ԫ��ÿ��ɶ��۳�10��������˵��������ǣ� ��
A.���۵��۽���15Ԫʱ��ÿ�����������
B.ÿ����������Ϊ1250Ԫ
C.�����۵��۽���10Ԫ��ÿ�������Ϊ1200Ԫ
D.��ÿ�������Ϊ1050Ԫ�������۵���һ��������5Ԫ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��������̶ӹ�ͬ�н�ij����·�������̣������ܳ�2000�ף��ס��ҷֱ�������������м�ʩ�����ƻ�ÿ���ʩ��6�ף�����������ͬ����֧����ÿ�ϸ����1������ʩ������ɱ���һ������ÿ�ϸ����1�ף�����ʩ���ɱ�Ϊ6��Ԫ����ÿ�ϸ����1�ף�����ʩ���ɱ�Ϊ8��Ԫ��
��1�������̽���ʱ����ʩ���ɱ������ڼ���ʩ���ɱ���![]() ��������ʩ�������ף�
��������ʩ�������ף�
��2��ʵ��ʩ����ʼ������������Ԥ�������ӣ���������ÿ��������ͳɱ��������仯����ÿ�ϸ����1������ʩ���ɱ�����m��Ԫʱ����ÿ��ɶ���![]() m�ף�����������ʣ���ʩ���ɱ����������£��ȼƻ�ÿ������
m�ף�����������ʣ���ʩ���ɱ����������£��ȼƻ�ÿ������![]() m�ף�������ÿ��ʵ���ܳɱ��ȼƻ��ࣨ11m-8����Ԫ����m��ֵ��
m�ף�������ÿ��ʵ���ܳɱ��ȼƻ��ࣨ11m-8����Ԫ����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
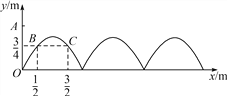
����Ŀ����ͼ������һ��ǽ�ϻ��Ƽ�����ͬ����������ͼ��������ͼ�е�ֱ������ϵ������ߵ������߿�����y��ax2��bx(a��0)��ʾ����֪��������B��C���㵽����ľ����Ϊ![]() m����ǽ��OA�ľ���ֱ�Ϊ
m����ǽ��OA�ľ���ֱ�Ϊ![]() m��
m��![]() m.
m.
(1)��Ò����ߵĺ�����ϵʽ������ͼ����ߵ㵽����ľ��룻
(2)����ǽ�ij���Ϊ10 m�����������������Ƽ��������Ē�������ͼ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ʵ��ķ����ⷽ�̡�
��1��4(x-3) ![]() =36
=36
��2��x2-4x��1��0.
��3��![]() -7x+6=0
-7x+6=0
��4��![]()
��5��(y��1)2��2y(1��y)��0.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ѫ�¡����л��������������ѫ��.��2019���á�����ѫ�¡��İ�λ�ܳ������У�����������Ҷ���Ԭ¡ƽ��������λԺʿ.��ͼ����λԺʿ�����μ�ΪA��B��C��D��Ϊ��ͬѧ���˽���λԺʿ�Ĺ��ף���ʦ������»��ȡ������ȫ��ͬ�Ŀ�Ƭ���ֱ�д��A��B��C��D�ĸ���ţ�Ȼ���泯�Ϸ��ã����Ⱥ�ÿ��ͬѧ�ɴ��������ȡһ�ţ����±�ź�Żأ���ʦҪ��ÿλͬѧ���ݳ鵽�Ŀ�Ƭ�ϵı�Ų�����ӦԺʿ����������С������С����С������ͬһλԺʿ���ϵĸ���.
A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���ס�����������ת����Ϸʱ���ֱ��ת��A��B�ֳ�3�ȷݺ�1�ȷݣ�����ÿһ���ڱ������֣���Ϸ����ͬʱת������ת�̣���ת��ֹͣ��ָ���������������֮��Ϊ����ʱ����ʤ��������֮��Ϊż��ʱ���һ�ʤ�����ָ��ǡ���ڷָ�����ʱ����������ת��ת�̣�
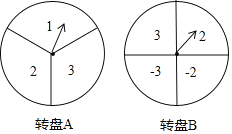
��1�����û���״ͼ���б��ķ��������ʤ�ĸ��ʣ�
��2�������Ϸ����Լס���˫����ƽ������ƽ����˵�����ɣ�������ƽ��������ת��A��ֻ��һ������ʹ��Ϸ��ƽ������Ҫ˵�����ɣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C��90����AB��13��BC��5����D��E�ֱ��ڱ�BC��AC�ϣ���BD��CE������CDE��DE���ۣ���C���ڵ�F������DF��AB����BD�ij�Ϊ_____��
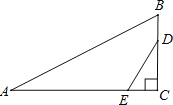
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com