
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§yЃНax2+bx+cжаЕФyгыxЕФВПЗжЖдгІжЕШчЯТБэЃК
x | Љ1 | 0 | 1 | 3 |
y | Љ3 | 1 | 3 | 1 |
ЯТСаНсТлжаЃКЂйХзЮяЯпЕФПЊПкЯђЯТЃЛЂкЦфЭМЯѓЕФЖдГЦжсЮЊxЃН1ЃЛЂлЕБxЃМ1ЪБЃЌКЏЪ§жЕyЫцxЕФдіДѓЖјдіДѓЃЛЂмЗНГЬax2+bx+cЃН0гавЛИіИљДѓгк4ЃЛЂнШєax12+bx1ЃНax22+bx2ЃЌЧвx1Ёйx2ЃЌдђx1+x2ЃН3ЃЌЦфжае§ШЗЕФНсТлга(ЁЁЁЁ)
A.ЂйЂкЂлB.ЂйЂкЂлЂмЂнC.ЂйЂлЂнD.ЂйЂлЂмЂн
ЁОД№АИЁПC
ЁОНтЮіЁП
РћгУХзЮяЯпЕФЖдГЦадЕУЕНХзЮяЯпЕФЖдГЦжсЮЊжБЯпx=![]() ЃЌдђПЩЖдЂкНјааХаЖЯЃЛРћгУКЏЪ§жЕЕФБфЛЏПЩШЗЖЈХзЮяЯпПЊПкЯђЯТЃЌдђПЩЖдЂйНјааХаЖЯЃЛИљОнЖўДЮКЏЪ§ЕФаджЪЖдЂлНјааХаЖЯЃЛРћгУХзЮяЯпЕФЖдГЦадШЗЖЈХзЮяЯпгыxжсЕФвЛИіНЛЕудкЃЈ3ЃЌ0ЃЉКЭЃЈ4ЃЌ0ЃЉжЎМфЃЌдђПЩЖдЂмНјааХаЖЯЃЎ
ЃЌдђПЩЖдЂкНјааХаЖЯЃЛРћгУКЏЪ§жЕЕФБфЛЏПЩШЗЖЈХзЮяЯпПЊПкЯђЯТЃЌдђПЩЖдЂйНјааХаЖЯЃЛИљОнЖўДЮКЏЪ§ЕФаджЪЖдЂлНјааХаЖЯЃЛРћгУХзЮяЯпЕФЖдГЦадШЗЖЈХзЮяЯпгыxжсЕФвЛИіНЛЕудкЃЈ3ЃЌ0ЃЉКЭЃЈ4ЃЌ0ЃЉжЎМфЃЌдђПЩЖдЂмНјааХаЖЯЃЎ
НтЃКгЩБэИёПЩжЊЃЌгЩБэИёПЩжЊЃЌxЃН0КЭxЃН3ЪБЃЌКЏЪ§жЕyЖМЪЧ1ЃЌ
ЁрХзЮяЯпЕФЖдГЦжсЮЊжБЯп![]() ЃЌ
ЃЌ
ЕБxЃН![]() ЪБЃЌЖўДЮКЏЪ§yЃНax2+bx+cШЁЕУзюДѓжЕЃЌ
ЪБЃЌЖўДЮКЏЪ§yЃНax2+bx+cШЁЕУзюДѓжЕЃЌ
ЁрХзЮяЯпЕФПЊПкЯђЯТЃЌЙЪЂйе§ШЗЃЌЂкДэЮѓЃЛ
ЕБxЃМ![]() ЪБЃЌyЫцxЕФдіДѓЖјдіДѓЃЌЙЪЂле§ШЗЃЌ
ЪБЃЌyЫцxЕФдіДѓЖјдіДѓЃЌЙЪЂле§ШЗЃЌ
ЗНГЬax2+bx+cЃН0ЕФвЛИіИљДѓгкЉ1ЃЌаЁгк0ЃЌдђЗНГЬЕФСэвЛИіИљДѓгк3ЃЌаЁгк4ЃЌЙЪЂмДэЮѓЃЌ
Шєax12+bx1ЃНax22+bx2ЃЌЧвx1Ёйx2ЃЌдђ![]() ЃЌ
ЃЌ
Ёрx1+x2ЃН3ЃЌЙЪЂне§ШЗЃЌ
ЙЪбЁЃКCЃЎ


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
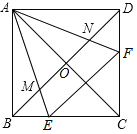
ЁОЬтФПЁПШчЭМЃЌЕуEЃЌFЗжБ№ЮЊе§ЗНаЮABCDЕФБпBCЃЌCDЩЯвЛЕуЃЌACЃЌBDНЛгкЕуOЃЌЧвЁЯEAF=45ЁуЃЌAEЃЌAFЗжБ№НЛЖдНЧЯпBDгкЕуMЃЌNЃЌдђгавдЯТНсТлЃКЂйЁЯAEB=ЁЯAEF=ЁЯANMЃЛЂкEF=BE+DFЃЛЂлЁїAOMЁзЁїADFЃЛЂмSЁїAEF=2SЁїAMNЃЌвдЩЯНсТлжаЃЌе§ШЗЕФЪЧ______ .ЃЈЧыАбе§ШЗНсТлЕФађКХЖМЬюЩЯЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
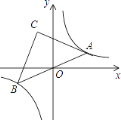
ЁОЬтФПЁПШчЭМЃЌдкЗДБШР§КЏЪ§y= ![]() ЕФЭМЯѓЩЯгавЛЖЏЕуAЃЌСЌНгAOВЂбгГЄНЛЭМЯѓЕФСэвЛжЇгкЕуBЃЌдкЕкЖўЯѓЯоФкгавЛЕуCЃЌТњзуAC=BCЃЌЕБЕуAдЫЖЏЪБЃЌЕуCЪМжедкКЏЪ§y=
ЕФЭМЯѓЩЯгавЛЖЏЕуAЃЌСЌНгAOВЂбгГЄНЛЭМЯѓЕФСэвЛжЇгкЕуBЃЌдкЕкЖўЯѓЯоФкгавЛЕуCЃЌТњзуAC=BCЃЌЕБЕуAдЫЖЏЪБЃЌЕуCЪМжедкКЏЪ§y= ![]() ЕФЭМЯѓЩЯдЫЖЏЃЌШєtanЁЯCAB=2ЃЌдђkЕФжЕЮЊЃЈ ЃЉ
ЕФЭМЯѓЩЯдЫЖЏЃЌШєtanЁЯCAB=2ЃЌдђkЕФжЕЮЊЃЈ ЃЉ
A. Љ3 B. Љ6 C. Љ9 D. Љ12
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌХзЮяЯп![]() ЃК
ЃК![]() НЛ
НЛ![]() жсгкЕу
жсгкЕу![]() ЃЌ
ЃЌ![]() ЃЌНЛ
ЃЌНЛ![]() жсгкЕу
жсгкЕу![]() .
.
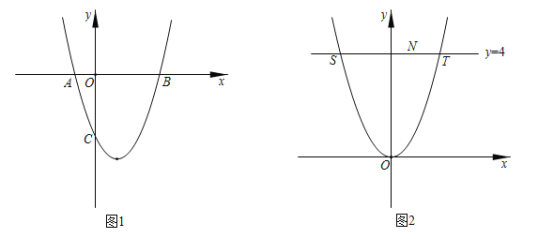
ЃЈ1ЃЉжБНгаДГіЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЕФШЁжЕЗЖЮЇЪЧ____________ЃЛ
ЕФШЁжЕЗЖЮЇЪЧ____________ЃЛ
ЃЈ2ЃЉЕу![]() дкХзЮяЯп
дкХзЮяЯп![]() ЩЯЃЌЧѓ
ЩЯЃЌЧѓ![]() ЕФУцЛ§ЃЛ
ЕФУцЛ§ЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌНЋХзЮяЯп![]() ЦНвЦЃЌЪЙЦфЖЅЕуЮЊдЕу
ЦНвЦЃЌЪЙЦфЖЅЕуЮЊдЕу![]() ЃЌЕУЕНХзЮяЯп
ЃЌЕУЕНХзЮяЯп![]() ЃЌжБЯп
ЃЌжБЯп![]() гыХзЮяЯп
гыХзЮяЯп![]() НЛгк
НЛгк![]() ЁЂ
ЁЂ![]() СНЕуЃЌЕу
СНЕуЃЌЕу![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЩЯвЛЖЏЕуЃЈВЛгы
ЩЯвЛЖЏЕуЃЈВЛгы![]() ЁЂ
ЁЂ![]() жиКЯЃЉЃЌЪдЬНОПХзЮяЯп
жиКЯЃЉЃЌЪдЬНОПХзЮяЯп![]() ЩЯЪЧЗёДцдкЕу
ЩЯЪЧЗёДцдкЕу![]() ЃЌЕу
ЃЌЕу![]() ЙигкЕу
ЙигкЕу![]() ЕФжааФЖдГЦЕу
ЕФжааФЖдГЦЕу![]() вВдкХзЮяЯп
вВдкХзЮяЯп![]() ЩЯ.
ЩЯ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвдABЮЊжБОЖЕФЁбOНЛЁЯBADЕФНЧЦНЗжЯпгкCЃЌЙ§CзїCDЁЭADгкDЃЌНЛABЕФбгГЄЯпгкEЃЎ
(1)ЧѓжЄЃКжБЯпCDЮЊЁбOЕФЧаЯпЃЛ
(2)ЕБABЃН2BEЃЌЧвCEЃН![]() ЪБЃЌЧѓADЕФГЄЃЎ
ЪБЃЌЧѓADЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвУЧЖЈвхСНИіВЛЯрНЛЕФКЏЪ§ЭМЯѓдкЪњжБЗНЯђЩЯЕФзюЖЬОрРыЮЊетСНИіКЏЪ§ЕФЁАКЭаГжЕЁБЃЎ
(1)ЧѓХзЮяЯпyЃНx2Љ2x+2гыxжсЕФЁАКЭаГжЕЁБЃЛ
(2)ЧѓХзЮяЯпyЃНx2Љ2x+2гыжБЯпyЃНxЉ1ЕФЁАКЭаГжЕЁБЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊШёНЧЁЯAOBШчЭМЃЌЃЈ1ЃЉдкЩфЯпOAЩЯШЁвЛЕуCЃЌвдЕуOЮЊдВаФЃЌOCГЄЮЊАыОЖзї![]() ЃЌНЛЩфЯпOBгкЕуDЃЌСЌНгCDЃЛ
ЃЌНЛЩфЯпOBгкЕуDЃЌСЌНгCDЃЛ
ЃЈ2ЃЉЗжБ№вдЕуCЃЌDЮЊдВаФЃЌCDГЄЮЊАыОЖзїЛЁЃЌНЛ![]() гкЕуMЃЌNЃЛ
гкЕуMЃЌNЃЛ
ЃЈ3ЃЉСЌНгOMЃЌMNЃЎ
ИљОнвдЩЯзїЭМЙ§ГЬМАЫљзїЭМаЮЃЌЯТСаНсТлжаДэЮѓЕФЪЧЃЈ ЃЉ

A. ЁЯCOM=ЁЯCODB. ШєOM=MNЃЌдђЁЯAOB=20Ёу
C. MNЁЮCDD. MN=3CD
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬГЁЯњЪлвЛХњГФЩРЃЌЦНОљУПЬьПЩЪлГі20МўЃЌУПМўгЏРћ40дЊЃЌОЙ§ЕїВщЗЂЯжЃЌЯњЪлЕЅМлУПНЕЕЭ5дЊЃЌУПЬьПЩЖрЪлГі10МўЃЌЯТСаЫЕЗЈДэЮѓЕФЪЧЃЈ ЃЉ
A.ЯњЪлЕЅМлНЕЕЭ15дЊЪБЃЌУПЬьЛёЕУРћШѓзюДѓ
B.УПЬьЕФзюДѓРћШѓЮЊ1250дЊ
C.ШєЯњЪлЕЅМлНЕЕЭ10дЊЃЌУПЬьЕФРћШѓЮЊ1200дЊ
D.ШєУПЬьЕФРћШѓЮЊ1050дЊЃЌдђЯњЪлЕЅМлвЛЖЈНЕЕЭСЫ5дЊ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁАЙВКЭЙњбЋеТЁБЪЧжаЛЊШЫУёЙВКЭЙњЕФзюИпШйгўбЋеТ.дк2019ФъЛёЕУЁАЙВКЭЙњбЋеТЁБЕФАЫЮЛНмГіШЫЮяжаЃЌгагкУєЁЂЫяМвЖАЁЂдЌТЁЦНЁЂЛЦаёЛЊЫФЮЛдКЪП.ШчЭМЪЧЫФЮЛдКЪПЃЈвРДЮМЧЮЊAЃЌBЃЌCЃЌDЃЉЮЊШУЭЌбЇУЧСЫНтЫФЮЛдКЪПЕФЙБЯзЃЌРЯЪІЩшМЦШчЯТЛюЖЏЃКШЁЫФеХЭъШЋЯрЭЌЕФПЈЦЌЃЌЗжБ№аДЩЯAЃЌBЃЌCЃЌDЫФИіБъКХЃЌШЛКѓБГУцГЏЩЯЗХжУЃЌНСдШКѓУПИіЭЌбЇПЩДгжаЫцЛњГщШЁвЛеХЃЌМЧЯТБъКХКѓЗХЛиЃЌРЯЪІвЊЧѓУПЮЛЭЌбЇИљОнГщЕНЕФПЈЦЌЩЯЕФБъКХВщевЯргІдКЪПЕФзЪСЯжЦзїаЁБЈЃЌЧѓаЁУїКЭаЁЛЊВщевЭЌвЛЮЛдКЪПзЪСЯЕФИХТЪ.
A.  B.
B.  C.
C.  D.
D. 
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com