
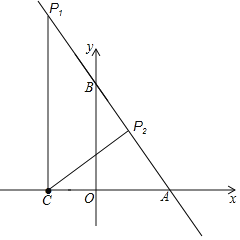
【题目】如图,在直角坐标平面xOy内,点A(6,0)、C(﹣4,0),过点A作直线AB,交y轴的正半轴于点B,且AB=10,点P是直线AB上的一个动点.
(1)求点B的坐标和直线AB的表达式;
(2)若以A、P、C为顶点的三角形与△AOB相似,求点P的坐标.

【答案】(1)直线AB的表达式为y=﹣![]() x+8;(2)点P的坐标为(﹣4,
x+8;(2)点P的坐标为(﹣4,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)由点A的坐标可得出OA的长,利用勾股定理可求出OB的长,结合点B在y轴正半轴上即可得出点B的坐标,由点A,B的坐标,再利用待定系数法即可求出直线AB的解析式;
(2)分△AOB∽△ACP和△AOB∽△APC两种情况考虑:①当△AOB∽△ACP时,∠ACP1=∠AOB=90°,利用一次函数图象上点的坐标特征可求出点P1的坐标;②当△AOB∽△APC时,设点P2的坐标为(m,﹣![]() m+8),利用相似三角形的性质可求出CP2的长,结合点C的坐标可得出关于m的方程,解之即可得出点P2的坐标.综上,此题得解.
m+8),利用相似三角形的性质可求出CP2的长,结合点C的坐标可得出关于m的方程,解之即可得出点P2的坐标.综上,此题得解.
解:(1)∵点A的坐标为(6,0),
∴OA=6,
∴OB=![]() =8.
=8.
∵点B在y轴的正半轴,
∴点B的坐标为(0,8).
设直线AB的表达式为y=kx+b(k≠0),
将A(6,0),B(0,8)代入y=kx+b,得:![]() ,
,
解得: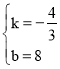 ,
,
∴直线AB的表达式为y=﹣![]() x+8.
x+8.
(2)分两种情况考虑,如图所示.
①当△AOB∽△ACP时,∠ACP1=∠AOB=90°,
当x=﹣4时,y=﹣![]() x+8=
x+8=![]() ,
,
∴点P1的坐标为(﹣4,![]() );
);
②当△AOB∽△APC时,设点P2的坐标为(m,﹣![]() m+8).
m+8).
∵点A的坐标为(6,0),点C的坐标为(﹣4,0),
∴AC=10.
∵△AOB∽△AP2C,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴CP2=8,
∴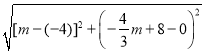 =8,
=8,
整理,得:(![]() m﹣4)2=0,
m﹣4)2=0,
解得:m=![]() ,
,
∴点P2的坐标为(![]() ,
,![]() ).
).
综上所述:点P的坐标为(﹣4,![]() )或(
)或(![]() ,
,![]() ).
).


 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
【题目】用适当的方法解方程。
(1)4(x-3) ![]() =36
=36
(2)x2-4x+1=0.
(3)![]() -7x+6=0
-7x+6=0
(4)![]()
(5)(y-1)2+2y(1-y)=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学复习课上,数学老师用几何画板上画出二次函数y=ax2+bx+c(a≠0)图象如图所示,四名同学根据图象,说出下列结论:李佳:abc<0:王宁:2a﹣b<0:孙浩:b2>4ac一帆:点(﹣3,y1),(1,y2)都在抛物线上,则有y1>y2,你认为其中正确的结论有( )
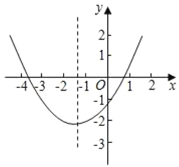
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富校园文化生活,提高学生的综合素质,促进中学生全面发展,学校开展了多种社团活动.小明喜欢的社团有:合唱社团、足球社团、书法社团、科技社团(分别用字母A,B,C,D依次表示这四个社团),并把这四个字母分别写在四张完全相同的不透明的卡片的正面上,然后将这四张卡片背面朝上洗匀后放在桌面上.
(1)小明从中随机抽取一张卡片是足球社团B的概率是 .
(2)小明先从中随机抽取一张卡片,记录下卡片上的字母后不放回,再从剩余的卡片中随机抽取一张卡片,记录下卡片上的字母.请你用列表法或画树状图法求出小明两次抽取的卡片中有一张是科技社团D的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
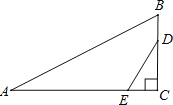
【题目】如图,在Rt△ABC中,∠C=90°,AB=13,BC=5,点D、E分别在边BC、AC上,且BD=CE,将△CDE沿DE翻折,点C落在点F处,且DF∥AB,则BD的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的解析式是y=x2﹣2x﹣3.
(1)与y轴的交点坐标是 ,顶点坐标是 .
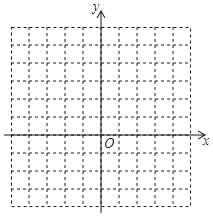
(2)在坐标系中利用描点法画出此抛物线;
x | … | … | |||||
y | … | … |
(3)结合图象回答:当﹣2<x<2时,函数值y的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利达经销店为某工厂代销一种建筑材料(这里的代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每下降10元时,月销售量就会增加7.5吨.综合考虑各种因素,每售出一吨建筑材料共需支付厂家及其它费用100元.
(1)当每吨售价是240元时,计算此时的月销售量;
(2)在遵循“薄利多销”的原则下,问每吨材料售价为多少时,该经销店的月利润为9000元?
(3)小静说:“当月利润最大时,月销售额也最大.”你认为对吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
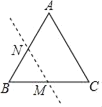
【题目】如图,在等边△ABC中,AB=4cm,点M为边BC的中点,点N为边AB上的任意一点(不与点A,B重合).若点B关于直线MN的对称点B'恰好落在等边△ABC的边上,则BN的长为_____cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com