
【题目】如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
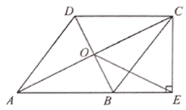
(1)求证:四边形ABCD是菱形;(2)若AE=5,OE=3,求线段CE的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)先判断出∠OAB=∠DCA,进而判断出∠DAC=∠DAC,得出CD=AD=AB,即可得出结论;
(2)四边形ABCD是菱形可得OA=OC,由直角三角形斜边中线等于斜边一半可知,在Rt△AEC中,AC=2OE=6,再由勾股定理求出CE..
解:(1)∵AB∥CD,
∴∠OAB=∠DCA,
∵AC为∠DAB的平分线,
∴∠OAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD=AB,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴ABCD是菱形;
(2)∵四边形ABCD是菱形,
∴OA=OC,
∵CE⊥AB,OE=3,
∴AC=2OE=6,
在Rt△AEC中,
∴CE=![]() =
=![]() =
=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两工程队共同承建某高速路隧道工程,隧道总长2000米,甲、乙分别从隧道两端向中间施工,计划每天各施工6米.因地质情况不同,两支队伍每合格完成1米隧道施工所需成本不一样.甲每合格完成1米,隧道施工成本为6万元;乙每合格完成1米,隧道施工成本为8万元.
(1)若工程结算时乙总施工成本不低于甲总施工成本的![]() ,求甲最多施工多少米?
,求甲最多施工多少米?
(2)实际施工开始后因地质情况比预估更复杂,甲乙两队每日完成量和成本都发生变化.甲每合格完成1米隧道施工成本增加m万元时,则每天可多挖![]() m米,乙因特殊地质,在施工成本不变的情况下,比计划每天少挖
m米,乙因特殊地质,在施工成本不变的情况下,比计划每天少挖![]() m米,若最终每天实际总成本比计划多(11m-8)万元,求m的值.
m米,若最终每天实际总成本比计划多(11m-8)万元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,甲、乙两人在玩转盘游戏时,分别把转盘A,B分成3等份和1等份,并在每一份内标上数字.游戏规则:同时转动两个转盘,当转盘停止后,指针所在区域的数字之积为奇数时,甲获胜;当数字之积为偶数时,乙获胜.如果指针恰好在分割线上时,则需重新转动转盘.
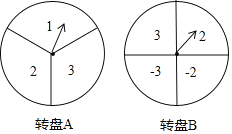
(1)利用画树状图或列表的方法,求甲获胜的概率.
(2)这个游戏规则对甲、乙双方公平吗?若公平,请说明理由;若不公平,请你在转盘A上只修改一个数字使游戏公平(不需要说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学复习课上,数学老师用几何画板上画出二次函数y=ax2+bx+c(a≠0)图象如图所示,四名同学根据图象,说出下列结论:李佳:abc<0:王宁:2a﹣b<0:孙浩:b2>4ac一帆:点(﹣3,y1),(1,y2)都在抛物线上,则有y1>y2,你认为其中正确的结论有( )
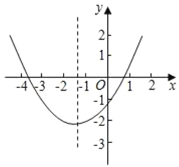
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】顺次连接一个四边形的各边中点,得到了一个矩形,则下列四边形中满足条件的是( )
①平行四边形;②菱形;③矩形;④对角线互相垂直的四边形.
A. ①③B. ②③C. ③④D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富校园文化生活,提高学生的综合素质,促进中学生全面发展,学校开展了多种社团活动.小明喜欢的社团有:合唱社团、足球社团、书法社团、科技社团(分别用字母A,B,C,D依次表示这四个社团),并把这四个字母分别写在四张完全相同的不透明的卡片的正面上,然后将这四张卡片背面朝上洗匀后放在桌面上.
(1)小明从中随机抽取一张卡片是足球社团B的概率是 .
(2)小明先从中随机抽取一张卡片,记录下卡片上的字母后不放回,再从剩余的卡片中随机抽取一张卡片,记录下卡片上的字母.请你用列表法或画树状图法求出小明两次抽取的卡片中有一张是科技社团D的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AB=13,BC=5,点D、E分别在边BC、AC上,且BD=CE,将△CDE沿DE翻折,点C落在点F处,且DF∥AB,则BD的长为_____.
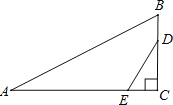
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利达经销店为某工厂代销一种建筑材料(这里的代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每下降10元时,月销售量就会增加7.5吨.综合考虑各种因素,每售出一吨建筑材料共需支付厂家及其它费用100元.
(1)当每吨售价是240元时,计算此时的月销售量;
(2)在遵循“薄利多销”的原则下,问每吨材料售价为多少时,该经销店的月利润为9000元?
(3)小静说:“当月利润最大时,月销售额也最大.”你认为对吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A是y轴上一点,其坐标为(0,6),点B在x轴的正半轴上.点P,Q均在线段AB上,点P的横坐标为m,点Q的横坐标大于m,在△PQM中,若PM∥x轴,QM∥y轴,则称△PQM为点P,Q的“肩三角形.
(1)若点B坐标为(4,0),且m=2,则点P,B的“肩三角形”的面积为 ;
(2)当点P,Q的“肩三角形”是等腰三角形时,求点B的坐标;
(3)在(2)的条件下,作过O,P,B三点的抛物线y=ax2+bx+c
①若M点必为抛物线上一点,求点P,Q的“肩三角形”面积S与m之间的函数关系式,并写出自变量m的取值范围.
②当点P,Q的“肩三角形”面积为3,且抛物线y=ax2+bx+c与点P,Q的“肩三角形”恰有两个交点时,直接写出m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com