
【题目】已知![]() (本题中的角均大于
(本题中的角均大于![]() 且小于
且小于![]() )
)
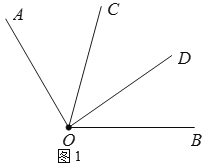
(1)如图1,在![]() 内部作
内部作![]() ,若
,若![]() ,求
,求![]() 的度数;
的度数;
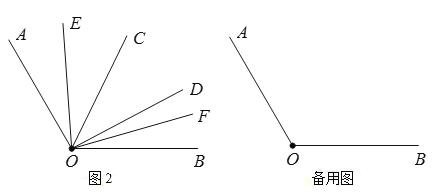
(2)如图2,在![]() 内部作
内部作![]() ,
,![]() 在
在![]() 内,
内,![]() 在
在![]() 内,且
内,且![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
(3)射线![]() 从
从![]() 的位置出发绕点
的位置出发绕点![]() 顺时针以每秒
顺时针以每秒![]() 的速度旋转,时间为
的速度旋转,时间为![]() 秒(
秒(![]() 且
且![]() ).射线
).射线![]() 平分
平分![]() ,射线
,射线![]() 平分
平分![]() ,射线
,射线![]() 平分
平分![]() .若
.若![]() ,则
,则![]() 秒.
秒.
【答案】(1)40;(2)84;(3)7.5或15或45
【解析】
(1)利用角的和差进行计算便可;
(2)设![]() ,则
,则![]() ,
,![]() ,通过角的和差列出方程解答便可;
,通过角的和差列出方程解答便可;
(3)分情况讨论,确定∠MON在不同情况下的定值,再根据角的和差确定t的不同方程进行解答便可.
解:(1))∵∠AOD+∠BOC=∠AOC+∠COD+∠BOD+∠COD=∠AOB+∠COD
又∵∠AOD+∠BOC=160°且∠AOB=120°
∴![]()
![]()
![]()
(2)![]() ,
,![]()
![]() 设
设![]() ,则
,则![]() ,
,![]()
则![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(3)当OI在直线OA的上方时,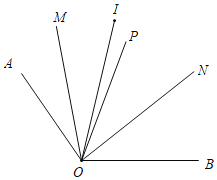
有∠MON=∠MOI+∠NOI=![]() (∠AOI+∠BOI))=
(∠AOI+∠BOI))=![]() ∠AOB=
∠AOB=![]() ×120°
×120°
∠PON=![]() ×60°=30°,
×60°=30°,
∵∠MOI=3∠POI,
∴3t=3(30-3t)或3t=3(3t-30),
解得t=![]() 或15;
或15;
当OI在直线AO的下方时,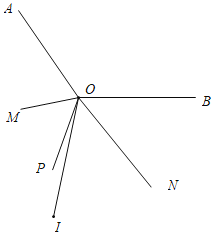
∠MON═![]() (360°-∠AOB)═
(360°-∠AOB)═![]() ×240°=120°,
×240°=120°,
∵∠MOI=3∠POI,
∴180°-3t=3(60°-![]() )或180°-3t=3(
)或180°-3t=3(![]() -60°),
-60°),
解得t=30或45,
综上所述,满足条件的t的值为![]() s或15s或30s或45s.
s或15s或30s或45s.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】为传播优秀数学文化,展现数学的内涵和魅力,提高学生的数学兴趣和素养,江苏教育出版社《时代学习报》与江苏省教育学会中学数学教学专业委员会共同举办初中数学文化节、初三数学应用与创新邀请赛,分别设有一、二、三等奖和纪念奖.某校参加此项比赛,获奖情况已汇制成如图所示的两幅不完整的统计图,根据图中所示信息解答下列问题:
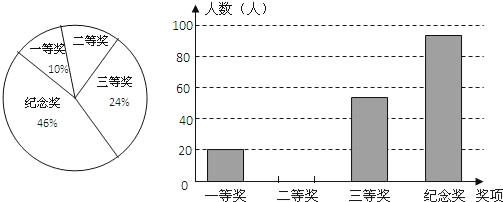
(1)该校一共有 名学生获奖;
(2)这次数学竞赛获二等奖人数是多少?
(3)请将条形统计图补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上的点A表示的数为6,点B表示的数为﹣4,点C到点A、点B的距离相等,动点P从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为x(x大于0)秒.
(1)点C表示的数是 ;
(2)当x= 秒时,点P到达点A处?
(3)运动过程中点P表示的数是 (用含字母x的式子表示);
(4)当P,C之间的距离为2个单位长度时,求x的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农科所甲、乙试验田各有水稻3万个,为了考察水稻穗长的情况,于同一天在这两块试验田里分别随机抽取了![]() 个稻穗进行测量,获得了它们的长度
个稻穗进行测量,获得了它们的长度![]() (单位:cm),并对数据(穗长)进行了整理、描述和分析.下面给出了部分信息.
(单位:cm),并对数据(穗长)进行了整理、描述和分析.下面给出了部分信息.
a.甲试验田穗长的频数分布统计表如下表所示(不完整):
甲试验田穗长频数分布表
分组/ | 频数 | 频率 |
| 4 | 0.08 |
| 9 | 0.18 |
|
| |
| 11 | 0.22 |
|
| 0.20 |
| 2 | |
合计 | 50 | 1.00 |
b.乙试验田穗长的频数分布直方图如图所示:
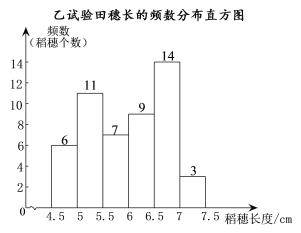
c.乙试验田穗长在![]() 这一组的是:
这一组的是:
6.3 6.4 6.3 6.3 6.2 6.2 6.1 6.2 6.4
d.甲、乙试验田穗长的平均数、中位数、众数、方差如下(表2):
试验田 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 5.924 | 5.8 | 5.8 | 0.454 |
乙 | 5.924 |
| 6.5 | 0.608 |
根据以上信息,回答下列问题:
(1)表中![]() 的值为 ,
的值为 ,![]() 的值为 ;
的值为 ;
(2)表中![]() 的值为 ;
的值为 ;
(3)在此次考察中,稻穗生长(长度)较稳定的试验田是 ;
A.甲 B.乙 C.无法推断
(4)若穗长在![]() 范围内的稻穗为“良好”,请估计甲试验田所有“良好”的水稻约为 万个.
范围内的稻穗为“良好”,请估计甲试验田所有“良好”的水稻约为 万个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 两点分别是
两点分别是![]() 轴和
轴和![]() 轴正半轴上两个动点,以三点
轴正半轴上两个动点,以三点![]() 为顶点的矩形
为顶点的矩形![]() 的面积为24,反比例函数
的面积为24,反比例函数![]() (
(![]() 为常数且
为常数且![]() )的图象与矩形
)的图象与矩形![]() 的两边
的两边![]() 分别交于点
分别交于点![]() .
.

(1)若![]() 且点
且点![]() 的横坐标为3.
的横坐标为3.
①点![]() 的坐标为 ,点
的坐标为 ,点![]() 的坐标为 (不需写过程,直接写出结果);
的坐标为 (不需写过程,直接写出结果);
②在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 的周长最小?若存在,请求出
的周长最小?若存在,请求出![]() 的周长最小值;若不存在,请说明理由.
的周长最小值;若不存在,请说明理由.
(2)连接![]() ,在点
,在点![]() 的运动过程中,
的运动过程中,![]() 的面积会发生变化吗?若变化,请说明理由,若不变,请用含
的面积会发生变化吗?若变化,请说明理由,若不变,请用含![]() 的代数式表示出
的代数式表示出![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个3×3的方格中填写了9个数字,使得每行、每列、每条对角线上的三个数之和相等,得到的3×3的方格称为一个三阶幻方.
(1)在图1中空格处填上合适的数字,使它构成一个三阶幻方;
(2)如图2的方格中填写了一些数和字母,当x+y的值为多少时,它能构成一个三阶幻方.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲和乙同时从学校放学,两人以各自送度匀速步行回家,甲的家在学校的正西方向,乙的家在学校的正东方向,乙家离学校的距离比甲家离学校的距离远3900米,甲准备一回家就开始做什业,打开书包时发现错拿了乙的练习册.于是立即步去追乙,终于在途中追上了乙并交还了练习册,然后再以先前的速度步行回家,(甲在家中耽搁和交还作业的时间忽略不计)结果甲比乙晚回到家中,如图是两人之间的距离y米与他们从学校出发的时间x分钟的函数关系图,则甲的家和乙的家相距_____米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com