
【题目】为传播优秀数学文化,展现数学的内涵和魅力,提高学生的数学兴趣和素养,江苏教育出版社《时代学习报》与江苏省教育学会中学数学教学专业委员会共同举办初中数学文化节、初三数学应用与创新邀请赛,分别设有一、二、三等奖和纪念奖.某校参加此项比赛,获奖情况已汇制成如图所示的两幅不完整的统计图,根据图中所示信息解答下列问题:
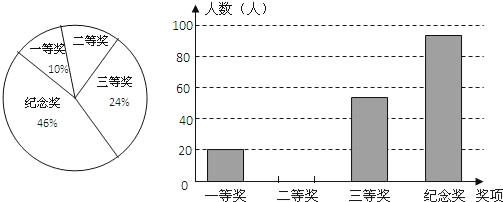
(1)该校一共有 名学生获奖;
(2)这次数学竞赛获二等奖人数是多少?
(3)请将条形统计图补充完整.
【答案】(1)200;(2)这次数学竞赛获二等奖人数是40人;(3)补图见解析.
【解析】试题分析:(1)用一等奖的人数除以对应的百分比求出该校共有多少学生获奖;
(2)根据三等奖、纪念奖的百分比分别求出三等奖、纪念奖的人数,然后用总的获奖人数减去一等奖、三等奖、纪念奖的人数即可得到二等奖的人数;
(3)根据(2)中二等奖的人数补全条形统计图即可.
试题解析:(1)获奖学生总人数为20÷10%=200(人),
故答案为:200;
(2)获三等奖人数为200×24%=48人,
纪念奖的人数为200×46%=92人,
这次数学竞赛获二等奖人数是200﹣(20+48+92)=40人;
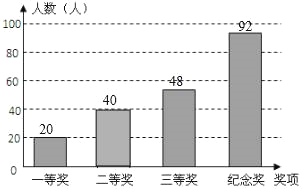
(3)补全条形图如下:


科目:初中数学 来源: 题型:
【题目】(本题满分10分)(1)问题发现
如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE,
填空:①∠AEB的度数为 ;
②线段AD、BE之间的数量关系是 .
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=900, 点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请判断∠AEB的度数及线段CM、AE、BE之间的数量关系,并说明理由.


(3)解决问题如图3,在正方形ABCD中,CD=![]() .若点P满足PD=1,且∠BPD=900,请直接写出点A到BP的距离.
.若点P满足PD=1,且∠BPD=900,请直接写出点A到BP的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两个不透明的袋子分别装有红、白两种颜色的球(除颜色不同外其余均相同),甲袋中有2个红球和1个白球,乙袋中有1个红球和3个白球.
(1)如果在甲袋中随机摸出一个小球,那么摸到红球的概率是______.
(2)如果在乙袋中随机摸出两个小球,那么摸到两球颜色相同的概率是______.
(3)如果在甲、乙两个袋子中分别随机摸出一个小球,那么摸到两球颜色相同的概率是多少?(请用列表法或树状图法说明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正整数按如图所示的规律排列下去,若用有序数对(m,n)表示从上到下第m排,从左到右第n个数,如(4,2)表示整数8.则(62,55)表示的数是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
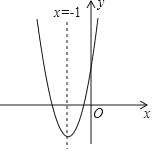
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,给出下列结论:
①b2=4ac;②abc>0;③a>c; ④4a﹣2b+c>0,其中正确有_____(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知:矩形ABCD的两边AB,BC的长是关于x的方程x2﹣mx+![]() =0的两个实数根.
=0的两个实数根.
(1)当m为何值时,矩形ABCD是正方形?求出这时正方形的边长;
(2)若AB的长为2,那么矩形ABCD的周长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在矩形 ABCD 中,动点 E 从点 A 出发,沿 AB→BC 方向运动,当点 E 到达点 C 时 停止运动.过点 E 作 FE⊥AE,交 CD 于 F 点,设点 E 运动路程为 x,FC=y,图②表示 y与 x 的函数关系的大致图像,则矩形 ABCD 的面积是( )

A. ![]() B. 5 C. 6 D.
B. 5 C. 6 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上有A、B、C三点,分别表示有理数-26,-10,10,动点P从A出发,以每秒1个单位的速度向终点C移动,设点P移动时间为t秒.
(1)用含t的代数式表示P点对应的数:__________;
用含t的代数式表示点P和点C的距离:PC=_____________.
(2)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回点A,
①点P、Q同时运动运动的过程中有__________处相遇,相遇时t=_______________秒.
②在点Q开始运动后,请用t的代数式表示P、Q两点间的距离.(友情提醒:注意考虑P、Q的位置)
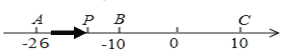
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() (本题中的角均大于
(本题中的角均大于![]() 且小于
且小于![]() )
)
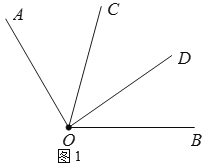
(1)如图1,在![]() 内部作
内部作![]() ,若
,若![]() ,求
,求![]() 的度数;
的度数;
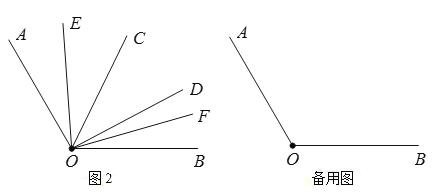
(2)如图2,在![]() 内部作
内部作![]() ,
,![]() 在
在![]() 内,
内,![]() 在
在![]() 内,且
内,且![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
(3)射线![]() 从
从![]() 的位置出发绕点
的位置出发绕点![]() 顺时针以每秒
顺时针以每秒![]() 的速度旋转,时间为
的速度旋转,时间为![]() 秒(
秒(![]() 且
且![]() ).射线
).射线![]() 平分
平分![]() ,射线
,射线![]() 平分
平分![]() ,射线
,射线![]() 平分
平分![]() .若
.若![]() ,则
,则![]() 秒.
秒.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com