
【题目】如图,在平面直角坐标系中,![]() 两点分别是
两点分别是![]() 轴和
轴和![]() 轴正半轴上两个动点,以三点
轴正半轴上两个动点,以三点![]() 为顶点的矩形
为顶点的矩形![]() 的面积为24,反比例函数
的面积为24,反比例函数![]() (
(![]() 为常数且
为常数且![]() )的图象与矩形
)的图象与矩形![]() 的两边
的两边![]() 分别交于点
分别交于点![]() .
.

(1)若![]() 且点
且点![]() 的横坐标为3.
的横坐标为3.
①点![]() 的坐标为 ,点
的坐标为 ,点![]() 的坐标为 (不需写过程,直接写出结果);
的坐标为 (不需写过程,直接写出结果);
②在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 的周长最小?若存在,请求出
的周长最小?若存在,请求出![]() 的周长最小值;若不存在,请说明理由.
的周长最小值;若不存在,请说明理由.
(2)连接![]() ,在点
,在点![]() 的运动过程中,
的运动过程中,![]() 的面积会发生变化吗?若变化,请说明理由,若不变,请用含
的面积会发生变化吗?若变化,请说明理由,若不变,请用含![]() 的代数式表示出
的代数式表示出![]() 的面积.
的面积.
【答案】(1)①点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ;②存在,周长
;②存在,周长![]() ;
;
(2)不变,![]() 的面积为
的面积为![]()
【解析】
(1)①求出点E的坐标,得出C点的纵坐标,根据面积为24即可求出C的坐标,得出F点横坐标即可求解;
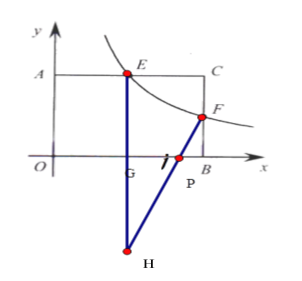
②作点E关于x轴的对称点G,连接GF,与x轴的交点为p,此时![]() 的周长最小
的周长最小
(2)先算出三角形![]() 与三角形
与三角形![]() 的面积,再求出三角形
的面积,再求出三角形![]() 的面积即可.
的面积即可.
(1)①点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ;
;
②作点E关于x轴的对称点G,连接GF,求与x轴的交点为p,此时![]() 的周长最小
的周长最小
由①得EF=![]()
由对称可得EP=PH,
由 H(3,-4) F(6,2)可得HF=3![]()
△PEF=EP+PF+EF=FH+EF=![]()
(2)不变,求出三角形![]() 与三角形
与三角形![]() 的面积为
的面积为![]()
求出三角形![]() 的面积为
的面积为![]()
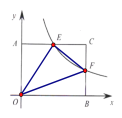
设E位(a, ![]() ),则S△AEO=
),则S△AEO=![]() ,同理可得S△AFB=
,同理可得S△AFB=![]() ,
,
∵矩形![]() 的面积为24
的面积为24
F(![]() ,
,![]() ),C(
),C(![]() ,
,![]() )
)
S△CEF=![]()
![]()
S![]() =24-
=24-![]() -k=
-k=![]() .
.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】己知:矩形ABCD的两边AB,BC的长是关于x的方程x2﹣mx+![]() =0的两个实数根.
=0的两个实数根.
(1)当m为何值时,矩形ABCD是正方形?求出这时正方形的边长;
(2)若AB的长为2,那么矩形ABCD的周长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是某同学在沙滩上用石于摆成的小房子,第一个图形由5个小石子组成,第二个图形由12个小石子组成,第三个图形由21个小石子组成,,观察图形的变化规律,第8个小房子用的小石子数量是( )

A.78B.96C.105D.108
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,二次函数y=ax2+bx的图象过点A(﹣1,3),顶点B的横坐标为1.

(1)求这个二次函数的表达式;
(2)点P在该二次函数的图象上,点Q在x轴上,若以A、B、P、Q为顶点的四边形是平行四边形,求点P的坐标;
(3)如图3,一次函数y=kx(k>0)的图象与该二次函数的图象交于O、C两点,点T为该二次函数图象上位于直线OC下方的动点,过点T作直线TM⊥OC,垂足为点M,且M在线段OC上(不与O、C重合),过点T作直线TN∥y轴交OC于点N.若在点T运动的过程中, ![]() 为常数,试确定k的值.
为常数,试确定k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() (本题中的角均大于
(本题中的角均大于![]() 且小于
且小于![]() )
)
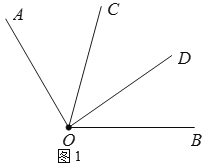
(1)如图1,在![]() 内部作
内部作![]() ,若
,若![]() ,求
,求![]() 的度数;
的度数;
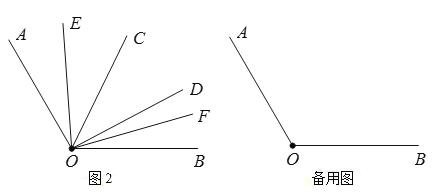
(2)如图2,在![]() 内部作
内部作![]() ,
,![]() 在
在![]() 内,
内,![]() 在
在![]() 内,且
内,且![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
(3)射线![]() 从
从![]() 的位置出发绕点
的位置出发绕点![]() 顺时针以每秒
顺时针以每秒![]() 的速度旋转,时间为
的速度旋转,时间为![]() 秒(
秒(![]() 且
且![]() ).射线
).射线![]() 平分
平分![]() ,射线
,射线![]() 平分
平分![]() ,射线
,射线![]() 平分
平分![]() .若
.若![]() ,则
,则![]() 秒.
秒.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分6分)某公司调查某中学学生对其环保产品的了解情况,随机抽取该校部分学生进行问卷,结果分“非常了解”、“比较了解”、“一般了解”、“不了解”四种类型,分别记为A、B、C、D.根据调查结果绘制了如下尚不完整的统计图. 
(1)本次问卷共随机调查了 名学生,扇形统计图中m= .
(2)请根据数据信息补全条形统计图;
(3)若该校有1000名学生,估计选择“非常了解”、“比较了解”共约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强想利用树影测树高,他在某一时刻测得直立的标杆长0.8m,其影长为1m,同时测树影时因树靠近某建筑物,影子不全落在地上,有一部分落在墙上如图,若此时树在地面上的影长为5.5m,在墙上的影长为1.5m,求树高

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:数a,b,c 在数轴上的对应点如下图所示,
(1)在数轴上表示﹣a;
(2)比较大小(填“<”或“>”或“=”):a+b 0,﹣3c 0,c﹣a 0;
(3)化简|a+b|﹣|﹣3c|﹣|c﹣a|.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,甲、乙两块边长为a米(a>1)的正方形田地,甲地修了两条互相垂直的宽为1米的通道,乙地正中间修了边长为1米的蓄水池,甲乙两田地的剩余地方全部种植小麦,一年后收获小麦m千克.(m>0)

(1)甲地的小麦种植面积为 平方米,乙地的小麦种植面积为 平方米;
(2)甲乙两地小麦种植面积较小的是 地;
(3)若高的单位面积产量是低的单位面积产量的![]() 倍,求a的值.
倍,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com